
已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D。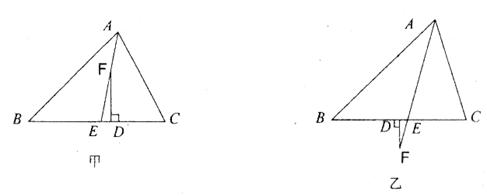
(1)试说明:∠EFD=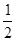 (∠C-∠B);
(∠C-∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由。
(1)通过角的负余证明。(2)成立
解析试题分析:(1)证明:∵FD⊥EC∴∠EFD=90°-∠FEC
∴∠FEC=∠B+∠BAE
又∵AE平分∠BAC
∴∠BAE=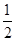 ∠BAC=
∠BAC=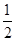 (180°-∠B-∠C)=90°-
(180°-∠B-∠C)=90°-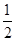 (∠B+∠C)
(∠B+∠C)
则∠EFD=90°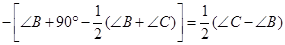
(2)∵AE平分∠BAC,∴∠BAE=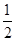 ∠BAC.
∠BAC.
∵∠BAC=180°-(∠B+∠C);
∴∠BAE=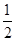 [180°-(∠B+∠C)];
[180°-(∠B+∠C)];
∴∠FED=∠B+∠BAE=∠B+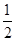 [180°-(∠B+∠C)]=90°+
[180°-(∠B+∠C)]=90°+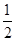 (∠B-∠C).
(∠B-∠C).
又∵FD⊥BC,∴∠FDE=90°;
∴∠EFD=90°-[90°+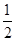 (∠B-∠C)=
(∠B-∠C)=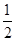 (∠C-∠B)].
(∠C-∠B)].
考点:角平分线的性质、三角形内角和定理和直角三角形的性质
点评:此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质,命题时经常将多个知识点联系在一起进行考查,这样更能训练学生的解题能力.


科目:初中数学 来源: 题型:
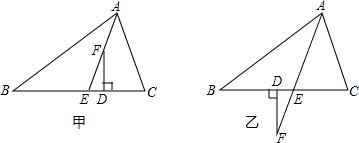 已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
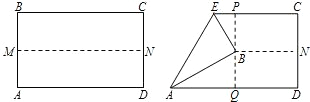
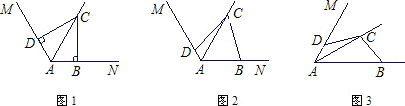
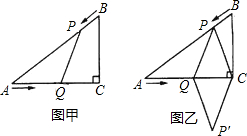
查看答案和解析>>
科目:初中数学 来源:2010年重庆市万州区初中数学教师专业知识竞赛试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2014届江西省吉安市七校八年级下学期联考数学试卷(解析版) 题型:解答题
已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D。
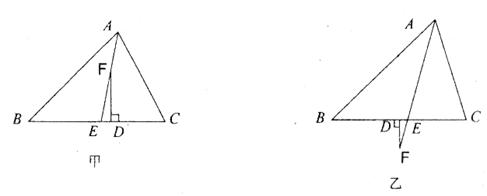
(1)试说明:∠EFD=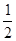 (∠C-∠B);
(∠C-∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com