
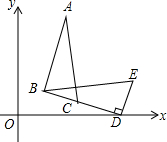
 如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$). 分析 作线段AB与BD的垂直平分线,它们的交点即为过A、B、D三点圆的圆心P,连接PD、PB、PE,过P作PF⊥x轴于F,利用旋转的性质得BC=DE,PB=PD,PE=PC,则可证明△PBC≌△PDE,所以∠PBC=∠PDE,易得∠PDB=∠PDE=$\frac{1}{2}$∠BDE=45°,于是可判断△PBD为等腰直角三角形,则PD=BD=3,然后在Rt△PDF中利用含30度的直角三角形三边的关系计算出DF和PF,从而可确定P点坐标.
解答 解:作线段AB与BD的垂直平分线,它们的交点即为过A、B、D三点圆的圆心P,连接PD、PB、PE,过P作PF⊥x轴于F,
∵△BDE旋转得到△ABC的位置,点C在BD上,
∴BC=DE,PB=PD,PE=PC,
在△PBC和PDE中,
$\left\{\begin{array}{l}{PB=PD}\\{BC=DE}\\{PC=PE}\end{array}\right.$,
∴△PBC≌△PDE,
∴∠PBC=∠PDE,
而PB=PD,
∴∠PBD=∠PDB,
∴∠PDB=∠PDE=$\frac{1}{2}$∠BDE=45°,
∴△PBD为等腰直角三角形,
∴PD=$\frac{\sqrt{2}}{2}$BD=3,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF=$\frac{1}{2}$PD=$\frac{1}{2}$×3=$\frac{3}{2}$,PF=$\sqrt{3}$DF=$\frac{3}{2}$$\sqrt{3}$,
∵点D的坐标是(5,0),
∴OF=OD-DF=5-$\frac{3}{2}$=$\frac{7}{2}$,
∴P点坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$),
故答案为:($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
点评 本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是证明△PBD为等腰直角三角形.


科目:初中数学 来源: 题型:解答题
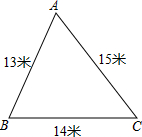 学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=16,则S2的值是$\frac{16}{3}$.
如图是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=16,则S2的值是$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
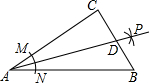 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是30.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是30.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com