
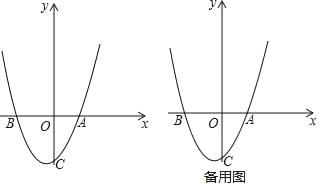
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),C(0,﹣5)三点,O为坐标原点.
(1)求此抛物线的解析式;
(2)把抛物线y=ax2+bx+c(a≠0)向上平移![]() 个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
【答案】(1)y=![]() x2+
x2+![]() x﹣5;(2)0<n<3;(3)PC=7或17.
x﹣5;(2)0<n<3;(3)PC=7或17.
【解析】
(1)设抛物线解析式为y=a(x﹣3)(x+5),将点C(0,﹣5)的坐标代入抛物线解析式中,利用待定系数法即可求得抛物线的解析式;
(2)先求得平移后新抛物线的顶点坐标,再根据新抛物线的顶点M在△ABC内求得n的取值范围;
(3)分点P在y轴负半轴上和点P在y轴正半轴上两种情况进行讨论,求出两种情况下CP的长度。
(1)∵抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),
∴设抛物线解析式为y=a(x﹣3)(x+5),
∵抛物线过点C(0,﹣5),∴a×(﹣3)×5=﹣5,
∴a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣3)(x+5)=
(x﹣3)(x+5)=![]() x2+
x2+![]() x﹣5,
x﹣5,
(2)记原抛物线的顶点为M',
由(1)知,抛物线解析式为y=![]() (x﹣3)(x+5)=
(x﹣3)(x+5)=![]() (x2+2x﹣15)=
(x2+2x﹣15)=![]() (x+1)2﹣
(x+1)2﹣![]() ,
,
∴M'(﹣1,﹣![]() ),
),
由平移知,M(﹣1﹣n,﹣1),
∵B(﹣5,0),C(0,﹣5),
∴直线BC的解析式为y=﹣x﹣5,
当y=﹣1时,﹣x﹣5=﹣1,
∴x=﹣4,
∴﹣4<﹣1﹣n<﹣1,
∴0<n<3;
(3)存在,
理由:①当P在y轴正半轴上时,如图,
过点P作PD⊥AC于D,
根据三角形的外角的性质得,∠OPA+∠OCA=∠PAD,
又∵∠OPA+∠OCA=∠CBA=45°,
∴∠PAD=∠CBA=45°,
∴AD=PD,
∵AO=3,CO=5,
∴AC=![]() ,
,
设AD=PD=m,则CD=AC+AD=m+![]() ,
,
又∵∠PDA=∠COA=90°,∠PCD=∠ACO,
∴△COA~△CDP,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]()
∴m=![]() ,
,
∴PC=![]() ×
×![]() =17,
=17,
②当P在y轴负半轴上时,记作P',
由①知,OP=PC﹣CO=17﹣5=12,取OP'=OP=12,如图,
则由对称知:∠OP'A=∠OPA, P'O=PO=12,
∴∠OP'A+∠OCA=∠OPA+∠OCA=∠CBA═45°,
同理P'也满足题目条件,∴P'C=OP'﹣OC=12﹣5=7,
综合以上得:PC=7或17.


科目:初中数学 来源: 题型:
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五关,分别用![]() 表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
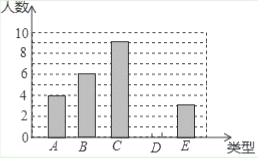
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、中位数;
(3)估计该单位750名职工共捐书多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() 与
与![]() 的“广益值”就等于
的“广益值”就等于![]() 的值,可记为
的值,可记为![]()
(1)在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,求
,求![]() ,
,![]() 的值.
的值.
(3)如图3,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m是正实数,关于x的方程2x2﹣mx﹣30=0的两个根为x1、x2,且5x1+3x2=0,在直角坐标系中,抛物线y=mx2+(4+k)x+k与x轴有_____个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,求x的取值范围;
时,求x的取值范围;
(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=x+b与反比例函数y=![]() 图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空)
图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
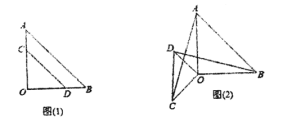
【题目】两块等腰直角三角尺![]() 与
与![]() (不全等)如图(1)放置,则有结论:①
(不全等)如图(1)放置,则有结论:①![]() ②
②![]() ;若把三角尺
;若把三角尺![]() 绕着点
绕着点![]() 逆时针旋转一定的角度后,如图(2)所示,判断结论:①
逆时针旋转一定的角度后,如图(2)所示,判断结论:①![]() ②
②![]() 是否都还成立?若成立请给出证明,若不成立请说明理由.
是否都还成立?若成立请给出证明,若不成立请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com