
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
【答案】(1)①50;②28;(2)①10.66;②12;③11;(3)我校八年级模拟体测中得12分的学生约有256人;
【解析】
(1)求直方图中各组人数和即可求得跳绳得学生人数,利用百分比的意义求得m即可;
(2)利用平均数、众数、中位数的定义求解即可;
(3)利用总人数乘以对应的百分比即可求得;
(1)本次抽取到的学生人数为:4+5+11+14+16=50(人);
m%=14![]() 50x100%=28%,
50x100%=28%,
∴![]() =28;
=28;
故答案为:①50;②28;
(2)观察条形统计图得,
本次调查获取的样本数据的平均数![]() ,
,
∴本次调查获取的样本数据的平均数为10.66,
∵在这组样本数据中,12出现了16次,
∴众数为12,
∵将这组数据按从小到大排列后,其中处于中间位置的两个数都为11,
∴中位数为:![]() ,
,
(3)800×32%=256人;
答:我校八年级模拟体测中得12分的学生约有256人;


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点E是边AD的中点.连接BE,在BE上找一点F,连接AF,将AF绕点A顺时针旋转90°到AG,点F与点G对应.AG、BD延长线交于点H.若AB=4,当F、E、G三点共线时,求S△BFH=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它们的相关函数为y= .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数y=﹣x2+4x﹣![]() .
.
①当点B(m, ![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数y=﹣x2+4x﹣![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生对待学习的态度一直是教育工作者关注的问题之一.为此市教育局对部分学校的九年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1) 此次抽样调查中,共调查了 名学生;并将图①补充完整;
(2) 求出图中②C级所占的圆心角的度数;
(3) 根据抽样调查结果,请你估计我市近50000名九年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
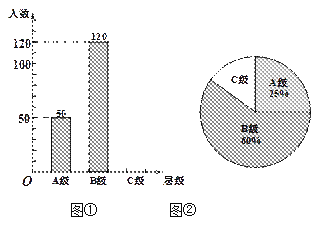
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂A,B两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A,B两种货厢的节数,有哪几种运输方案?请设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,BC=12,E为边AC的中点,
(1)如图1,过点E作EH⊥BC,垂足为点H,求线段CH的长;
(2)作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F.
①如图2,当∠BAC=90°时,求BD的长;
②如图3,设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
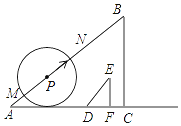
【题目】如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com