Question

17．将A（3，2），B为x轴上一点，O为坐标原点，若△AOB是等腰三角形，求B点坐标．

Answer 1

分析 根据等腰三角形的性质，要使△AOB等腰三角形，可以分三种情况考虑：①以OA=AB时，②OA=OB时，③OB=AB时，画出图形，求出即可．

解答 解：有三种情况：①如图1，以A为圆心，以OA为半径画弧，交x轴于B（O除外），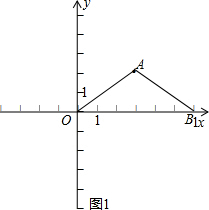

此时OA=AB，B点的坐标为（6，0），
②如图1，以O为圆心，以OA为半径画弧，交x轴于两点，

此时OA=OB，
∵A（3，2），
∴OA=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$，此时B点的坐标为（$\sqrt{13}$，0）或（-$\sqrt{13}$，0），
③作OA的垂直平分线，交x轴于B₄，此时OB=AB，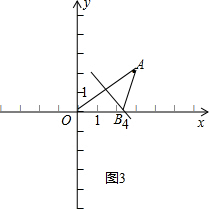

设B的坐标为（x，0），
∵A（3，2），O（0，0），
∴x²+（0-2）²=（x-3）²+（0-2）²，
解得：x=1.5，
此时B的坐标为（1.5，0），
所以B点坐标为（6，0）或（$\sqrt{13}$，0）或（-$\sqrt{13}$，0）或（1.5，0）．

点评 本题考查了等腰三角形的定义，运用数形结合的思想进行解决，难度适中．