

分析 (1)求出∠3=∠4,∠BOP=∠PED=90°,根据AAS证△BPO≌△PDE即可;
(2)求出∠ABP=∠4,求出△ABP≌△CPD,即可得出答案;
(3)设OP=CP=a,求出AP=3a,CD=$\sqrt{2}$a,即可得出答案.
解答 (1)证明:∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBC-∠1,∠4=∠2-∠C,
∴∠3=∠4,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中
∵$\left\{\begin{array}{l}∠3=∠4\\∠BOP=∠PED\\ BP=PD\end{array}\right.$,
∴△BPO≌△PDE(AAS);
(2)证明:由(1)可得:∠3=∠4,
∵BP平分∠ABO,
∴∠ABP=∠3,
∴∠ABP=∠4,
在△ABP和△CPD中
∵$\left\{\begin{array}{l}∠A=∠C\\∠ABP=∠4\\ PB=CD\end{array}\right.$,
∴△ABP≌△CPD(AAS),
∴AP=CD.
(3)解:x与y的数量关系是x=$\frac{\sqrt{2}}{3}$y.
理由:如图,设OP=PC=a,则AO=OC=2a=BO,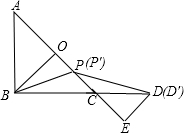
则AP=2a+a=3a,
由△OBP≌△EPD,得BO=PE,
PE=2a,CE=2a-a=a,
∵∠E=90°,∠ECD=∠ACB=45°,
∴DE=a,由勾股定理得:CD=$\sqrt{2}$a,
即y=3a,x=$\sqrt{2}$a,
∴x与y的数量关系是x=$\frac{\sqrt{2}}{3}$y.
点评 本题考查了全等三角形的性质和判定,等腰直角三角形性质,等腰三角形性质等知识点的综合应用,主要考查学生的推理和计算能力.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:解答题
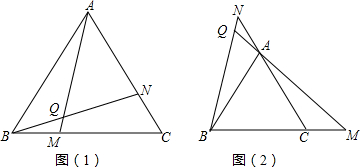
 如图,BF是△ABC的角平分线,AM⊥BF于M,CE平分△ABC的外角,AN⊥CE于N,
如图,BF是△ABC的角平分线,AM⊥BF于M,CE平分△ABC的外角,AN⊥CE于N,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
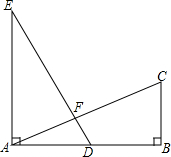 如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列式中成立的有( )
如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列式中成立的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com