
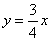 与BC边相交于点D。
与BC边相交于点D。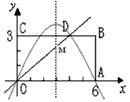
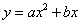 经过D、A两点,试确定此抛物线的函数表达式;
经过D、A两点,试确定此抛物线的函数表达式;解:(1)直线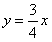 与BC交于点D(x,3), 与BC交于点D(x,3),把y=3代入  中得,x=4, 中得,x=4,∴D(4,3)。 (2)∵抛物线y=ax2+bx经过D(4,3)、A(6,0)两点, 把x=4,y=3;x=6,y=0分别代入y=ax2+bx中得, 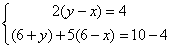 ,解得: ,解得: , ,∴抛物线的解析式为: 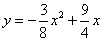 。 。(3)因△POA底边OA=6, ∴当S△POA有最大值时,点P须位于抛物线的最高点, ∵ 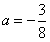 <0, <0,∴抛物线顶点恰为最高点, ∵  , ,∴  的最大值为 的最大值为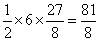 。 。 |
|
| (4)抛物线的对称轴与x轴的交点Q1符合条件, ∵CB∥OA,∠Q1OM=∠CDO, ∴Rt△Q1OM∽Rt△CDO, ∵ 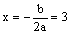 ,该点坐标为Q1(3,0), ,该点坐标为Q1(3,0),过点O作OD的垂线交抛物线的对称轴于点Q2, ∵对称轴平行于y轴, ∴∠Q2MO=∠DOC, ∴Rt△Q2MO∽Rt△DOC, 在Rt△Q2Q1O和Rt△DCO中, Q1O=CO=3,∠Q2=∠ODC, ∴Rt△Q2Q1O≌Rt△DCO, ∴CD=Q1Q2=4, ∵点Q2位于第四象限, ∴Q2(3,-4), 因此,符合条件的点有两个, 分别是Q1(3,0),Q2(3,-4)。 |
 |


科目:初中数学 来源: 题型:
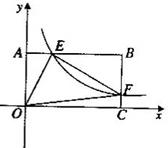
如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数![]() 的图象与边BC交于点F。
的图象与边BC交于点F。
1.若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求![]() 的值:
的值:
2.若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分10分)如图,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、B重合),过点E的反比例函数![]() 的图象与边BC交于点F.
的图象与边BC交于点F.

(1)若△OAE、△OCF的而积分别为![]() .且
.且![]() ,求k的值.
,求k的值.
(2)若OA=2,0C=4,问当点E运动到什么位置时,四边形OAEF的面积最大,其最大值为多少?
查看答案和解析>>
科目:初中数学 来源:2012届山东省宁津县实验中学九年级中考模拟数学试卷(带解析) 题型:解答题
如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数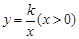 的图象与边BC交于点F。
的图象与边BC交于点F。
【小题1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求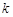 的值:
的值:
【小题2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省九年级中考模拟数学试卷(解析版) 题型:解答题
如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数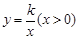 的图象与边BC交于点F。
的图象与边BC交于点F。
1.若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求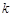 的值:
的值:
2.若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?

查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省荆门市东宝区中考模拟数学卷 题型:解答题
(本小题满分10分)如图,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、B重合),过点E的反比例函数 的图象与边BC交于点F.
的图象与边BC交于点F.

(1)若△OAE、△OCF的而积分别为 .且
.且 ,求k的值.
,求k的值.
(2)若OA=2,0C=4,问当点E运动到什么位置时,四边形OAEF的面积最大,其最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com