
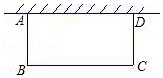
 欲用长为50m的篱笆,一面靠墙(墙的长度是20m),围成一个长方形花圃,设BC边的长为xm,花圃的面积为ym2,求:
欲用长为50m的篱笆,一面靠墙(墙的长度是20m),围成一个长方形花圃,设BC边的长为xm,花圃的面积为ym2,求:分析 (1)先表示AB=$\frac{50-x}{2}$,代入长方形面积公式可求出y关于x的函数解析式y=-$\frac{1}{2}{x}^{2}$+25x;
(2)根据墙的长度是20m得出x的取值为:x≤20,利用配方法将解析式化为顶点式,根据二次项系数为负数写出抛物线的增减性,当x<25时,y随x的增大而增大,得当x=20时,y有最大值,代入计算即可.
解答 解:(1)由题意得:AB=$\frac{50-x}{2}$=-$\frac{1}{2}$x+25,
y=AB•BC=x(-$\frac{1}{2}$x+25)=-$\frac{1}{2}{x}^{2}$+25x,
∴y关于x的函数解析式:y=-$\frac{1}{2}{x}^{2}$+25x;
(2)∵墙的长度是20m,
∴x≤20,
y=-$\frac{1}{2}{x}^{2}$+25x=-$\frac{1}{2}$(x2-50x+625-625)=-$\frac{1}{2}$(x-25)2+312.5,
∵-$\frac{1}{2}$<0,
∴当x<25时,y随x的增大而增大,
∴当x=20时,y有最大值,
y最大值=-$\frac{1}{2}$(20-25)2+312.5=300,
答:围成的花圃面积最大是300m2.
点评 本题是二次函数的应用,属于几何图形面积问题,考查了二次函数的性质及长方形面积,此类题利用面积公式可求得解析式,根据墙长得自变量x的取值,最大值问题就是二次函数的顶点问题,与图形相结合,本题中的二次函数的顶点不符合最大值,即不在取值范围内,因此这时的最大值根据增减性来判断.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
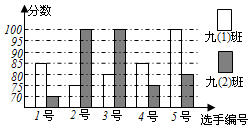 某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
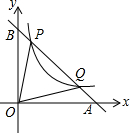 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于P、Q(4,m)两点,与两坐标轴交于A、B两点,点(0.5,8)在双曲线上.
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于P、Q(4,m)两点,与两坐标轴交于A、B两点,点(0.5,8)在双曲线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com