
【题目】有一个运算装置,当输入值为x时,其输出值为y,且y是x的二次函数,已知输入值为﹣2,0,1时,相应的输出值分别为5,﹣3,﹣4. 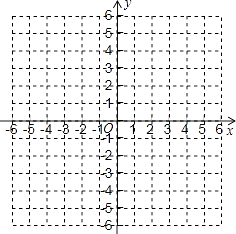
(1)求此二次函数的解析式;
(2)在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时输入值x的取值范围.
科目:初中数学 来源: 题型:
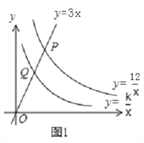
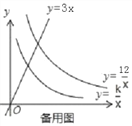
【题目】如图1,已知直线y=3x分别与双曲线y=![]() 、y=
、y=![]() (x>0)交于P、Q两点,且OP=2OQ.
(x>0)交于P、Q两点,且OP=2OQ.
(1)求k的值.
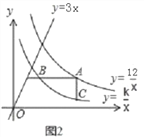
(2)如图2,若点A是双曲线y= ![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=
上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=![]() (x>0)于点B、C,连接BC.请你探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
(x>0)于点B、C,连接BC.请你探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
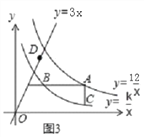
(3)如图3,若点D是直线y=3x上的一点,请你进一步探索在点A运动过程中,以点A、B、C、D为顶点的四边形能否为平行四边形?若能,求出此时点A的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地盛产柑桔,
两地盛产柑桔,![]() 地有柑桔200吨,
地有柑桔200吨,![]() 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知![]() 仓库可储存240吨,
仓库可储存240吨,![]() 仓库可储存260吨;从
仓库可储存260吨;从![]() 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从![]() 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从![]() 地运往
地运往![]() 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;
| C | D | 总计 |
A | x吨 | 200吨 | |
B | 300吨 | ||
总计 | 240吨 | 260吨 | 500吨 |
(2)试讨论A,B两地中,哪个运费较少;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.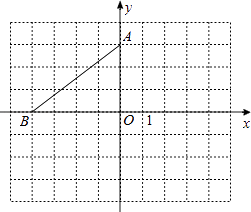
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5. 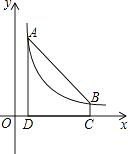
(1)求反比例函数的表达式和点B的坐标;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
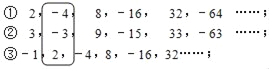
取每一行的第n个数,依次记为x、y、z.如上图中,当n=2时,x=﹣4,y=﹣3,z=2.
(1)当n=7时,请直接写出x、y、z的值,并求这三个数中最大的数与最小的数的差;
(2)已知n为偶数,且x、y、z这三个数中最大的数与最小的数的差为384,求n的值;
(3)若m=x+y+z,则x、y、z这三个数中最大的数与最小的数的差为 (用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是( ) 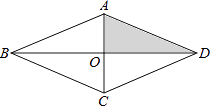
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PF⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中结论正确的个数是( )
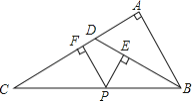
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com