
【题目】如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.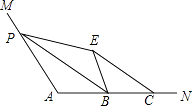
科目:初中数学 来源: 题型:
【题目】某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A,B,C,D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整)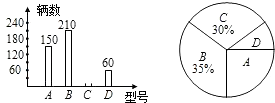
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整;
(3)若该专卖店计划订购这四款型号的电动自行车1800辆,求C型电动自行车应订购多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计费;月用水量超过20m3时,超过部分按2.6元/m3计费.设每户家庭的月用水量为xm3时,应交水费y元.
(1)试求出0≤x≤20和x>20时,y与x之间的函数关系;
(2)小明家第二季度用水量的情况如下:
月份 | 四月 | 五月 | 六月 |
用水量(m3) | 15 | 17 | 21 |
小明家这个季度共缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A,点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB2 . 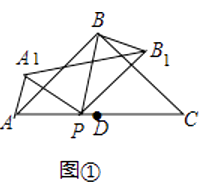
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;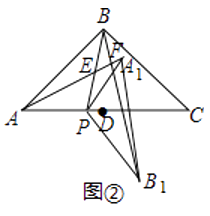
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB= ![]() ,设AP=x,求y关于x的函数关系式.
,设AP=x,求y关于x的函数关系式.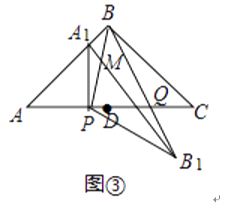
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB两端点坐标分别为A(![]() ),B(
),B(![]() ),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
A.A1(1,8),B1(-2,5)B.A1(3,2),B1(0,-1)
C.A1(-3,8),B1(-6,5)D.A1(-5,2),B1(-8,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:
(1)实践:如图1, ![]() 中,
中,![]() 为
为![]() 边上的中线,
边上的中线,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() .则
.则![]() .
.

(2)探究:在图2中,![]() 、
、![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 、
、![]() 的中点,四边形
的中点,四边形![]() 的面积记为
的面积记为![]() ,阴影部分面积记为
,阴影部分面积记为![]() ,则
,则![]() 和
和![]() 之间满足的关系式为______:
之间满足的关系式为______:
(3)解决问题:
在图3中,![]() 、
、![]() 、
、![]() 、
、![]() 分别为任意四边形
分别为任意四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,并且图中阴影部分的面积为
的中点,并且图中阴影部分的面积为![]() 平方厘米,求图中四个小三角形的面积和,并说明理由.
平方厘米,求图中四个小三角形的面积和,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;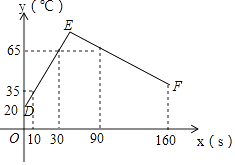
(1)当时间为20s、100s时,该食物的温度分别为℃,℃;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)时间是多少时,该食物的温度最高?最高是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com