
°æƒø°øƒ≥±£Ω°∆∑≥ß√øÃÏ…˙≤˙A£¨B¡Ω÷÷∆∑≈∆µƒ±£Ω°∆∑π≤600∆ø£¨A£¨B¡Ω÷÷≤˙∆∑√ø∆øµƒ≥…±æ∫Õ €º€»Áœ¬±Ì£¨…Ë√øÃÏ…˙≤˙A≤˙∆∑x∆ø£¨…˙≤˙’‚¡Ω÷÷≤˙∆∑√øÃÏπ≤ªÒ¿˚y‘™£Æ
A | °°B | |
≥…±æ£®‘™£©/∆ø | 50 | °°35 |
€º€£®‘™£©/∆ø | 70 | °°°°°°50 |
£®1£©«Î«Û≥ˆyπÿ”⁄xµƒ∫Ø ˝πÿœµ£ª
£®2£©∏√≥ß√øÃÏ…˙≤˙µƒA£¨B¡Ω÷÷≤˙∆∑±ªƒ≥æ≠œ˙…û´≤ø∂©π∫£¨≥ߺ“∂‘B≤˙∆∑≤ª±‰£¨∂‘A≤˙∆∑Ω¯––»√¿˚£¨√ø∆ø¿˚»ÛΩµµÕ![]() ‘™£¨≥ߺ“»Á∫Œ…˙≤˙ø… π√øÃϪҿ˚◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
‘™£¨≥ߺ“»Á∫Œ…˙≤˙ø… π√øÃϪҿ˚◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
°æ¥∞∏°ø£®1£©yπÿ”⁄xµƒ∫Ø ˝πÿœµŒ™£∫y£Ω5x+9000£ª£®2£©√øÃÏ…˙≤˙A≤˙∆∑250º˛£¨B≤˙∆∑350º˛ªÒ¿˚◊Ó¥Û£¨◊Ó¥Û¿˚»ÛŒ™9625‘™£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚£¨º¥ø…µ√yπÿ”⁄xµƒ∫Ø ˝πÿœµ ΩŒ™£∫y£Ω£®70©Å50£©x+£®50©Å35£©£®600©Åx£©£¨»ª∫۪غں¥ø…«Ûµ√¥∞∏£ª
£®2£© ◊œ»±Ì æ≥ˆªÒ¿˚”Îx÷ƺ‰µƒπÿœµΩ¯∂¯µ√≥ˆ∫Ø ˝◊Ó÷µ£Æ
£®1£©”…“‚µ√£∫
y£Ω£®70©Å50£©x+£®50©Å35£©£®600©Åx£©
£Ω5x+9000
°ýyπÿ”⁄xµƒ∫Ø ˝πÿœµŒ™£∫y£Ω5x+9000£ª
£®2£©”…“‚µ√£∫
y£Ω£®70©Å50©Å![]() £©x+£®50©Å35£©£®600©Åx£©
£©x+£®50©Å35£©£®600©Åx£©
£Ω©Å![]() £®x©Å250£©2+9625
£®x©Å250£©2+9625
°þ©Å![]() £º0
£º0
°ýµ±x£Ω250 ±£¨y”–◊Ó¥Û÷µ9625
°ý√øÃÏ…˙≤˙A≤˙∆∑250º˛£¨B≤˙∆∑350º˛ªÒ¿˚◊Ó¥Û£¨◊Ó¥Û¿˚»ÛŒ™9625‘™£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄’˝∑Ω–Œ![]() ÷–£¨
÷–£¨![]() «±þ
«±þ![]() …œ“ªµ„£®µ„
…œ“ªµ„£®µ„![]() ≤ª”ε„
≤ª”ε„![]() °¢
°¢![]() ÷ÿ∫œ£©£¨¡¨Ω·
÷ÿ∫œ£©£¨¡¨Ω·![]() .»ÁÕº¢Ÿ£¨π˝µ„
.»ÁÕº¢Ÿ£¨π˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() .“◊÷§
.“◊÷§![]() .£®≤ª–Ë“™÷§√˜£©»ÁÕº¢⁄£¨»°
.£®≤ª–Ë“™÷§√˜£©»ÁÕº¢⁄£¨»°![]() µƒ÷–µ„
µƒ÷–µ„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨Ωª
£¨Ωª![]() ”⁄µ„
”⁄µ„![]() .
.
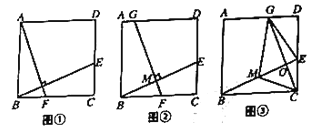
£®1£©«Û÷§£∫![]() .
.
£®2£©¡¨Ω·![]() £¨»Ù
£¨»Ù![]() £¨«Û
£¨«Û![]() µƒ≥§.
µƒ≥§.
£®3£©»ÁÕº¢€£¨»°![]() µƒ÷–µ„
µƒ÷–µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() .π˝µ„
.π˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() °¢
°¢![]() .»Ù
.»Ù![]() £¨«ÛÀƒ±þ–Œ
£¨«ÛÀƒ±þ–Œ![]() µƒ√ʪ˝.
µƒ√ʪ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Œ™¡À¡ÀΩ‚≥ı÷–∏˜ƒÍº∂—ß…˙√øÃϵƒ∆Ωæ˘ÀØ√þ ±º‰£®µ•Œª£∫h£¨æ´»∑µΩ1 h£©£¨≥È—˘µ˜≤È¡À≤ø∑÷—ß…˙£¨≤¢”√µ√µΩµƒ ˝æðªÊ÷∆¡Àœ¬√Ê¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ
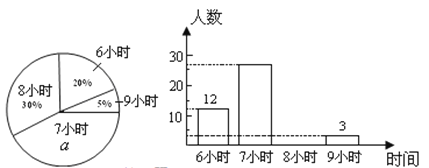
«Îƒ„∏˘æðÕº÷–Ã·π©µƒ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©«Û≥ˆ…»–ŒÕ≥º∆Õº÷–∞Ÿ∑÷ ˝![]() µƒ÷µŒ™_______£¨À˘≥È≤ȵƒ—ß…˙»À ˝Œ™______£ª
µƒ÷µŒ™_______£¨À˘≥È≤ȵƒ—ß…˙»À ˝Œ™______£ª
£®2£©«Û≥ˆ∆Ωæ˘ÀØ√þ ±º‰Œ™8–° ±µƒ»À ˝£¨≤¢≤π»´Ãı–ŒÕº£ª
£®3£©«Û≥ˆ’‚≤ø∑÷—ß…˙µƒ∆Ωæ˘ÀØ√þ ±º‰µƒ∆Ωæ˘ ˝£ª
£®4£©»Áπ˚∏√–£π≤”–—ß…˙1200√˚£¨«Îƒ„π¿º∆ÀØ√þ≤ª◊„£®…Ÿ”⁄8–° ±£©µƒ—ß…˙ ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
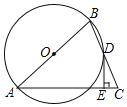
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨µ„D‘⁄BC…œ£¨
£¨µ„D‘⁄BC…œ£¨![]() £¨π˝µ„D◊˜
£¨π˝µ„D◊˜![]() £¨¥π◊„Œ™E£¨
£¨¥π◊„Œ™E£¨![]() æ≠π˝A£¨B£¨D»˝µ„£Æ
æ≠π˝A£¨B£¨D»˝µ„£Æ
![]() «Û÷§£∫AB «
«Û÷§£∫AB «![]() µƒ÷±æ∂£ª
µƒ÷±æ∂£ª
![]() ≈–∂œDE”Î
≈–∂œDE”Î![]() µƒŒª÷√πÿœµ£¨≤¢º”“‘÷§√˜£ª
µƒŒª÷√πÿœµ£¨≤¢º”“‘÷§√˜£ª
![]() »Ù
»Ù![]() µƒ∞Îæ∂Œ™10m£¨
µƒ∞Îæ∂Œ™10m£¨![]() £¨«ÛDEµƒ≥§£Æ
£¨«ÛDEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() £®
£®![]() £©æ≠π˝µ„
£©æ≠π˝µ„![]() £¨”Î
£¨”Î![]() ÷·µƒ∏∫∞Î÷·Ωª”⁄µ„
÷·µƒ∏∫∞Î÷·Ωª”⁄µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨«“
£¨«“![]() £¨≈◊ŒÔœþµƒ∂•µ„Œ™
£¨≈◊ŒÔœþµƒ∂•µ„Œ™![]() £Æ
£Æ

£®1£©«Û’‚Ãı≈◊ŒÔœþµƒ±Ì¥Ô Ω£ª
£®2£©¡™Ω·![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() £¨«ÛÀƒ±þ–Œ
£¨«ÛÀƒ±þ–Œ![]() µƒ√ʪ˝£ª
µƒ√ʪ˝£ª
£®3£©»Áπ˚µ„![]() ‘⁄
‘⁄![]() ÷·µƒ’˝∞Î÷·…œ£¨«“
÷·µƒ’˝∞Î÷·…œ£¨«“![]() £¨«Ûµ„
£¨«Ûµ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþy£Ω©Å![]() x2©Å
x2©Å![]() x+2
x+2![]() ”Îx÷·Ωª”⁄µ„A£¨B£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨¡¨Ω”AC£Æ
”Îx÷·Ωª”⁄µ„A£¨B£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨¡¨Ω”AC£Æ
£®1£©«Û÷±œþACµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº1£¨µ„PŒ™÷±œþAC…œ∑Ω≈◊ŒÔœþ…œ“ª∂ص„£¨π˝P◊˜PD°ÕAB£¨ΩªAC”⁄µ„E£¨µ„F «œþ∂ŒAC…œ“ª∂ص„£¨¡¨Ω”DF£Æµ±°˜PACµƒ√ʪ˝◊Ó¥Û ±£¨«ÛDF+![]() AFµƒ◊Ó–°÷µ£ª
AFµƒ◊Ó–°÷µ£ª
£®3£©»ÁÕº2£¨Ω´°˜OBC»∆◊≈µ„OÀ≥ ±’Ζ˝◊™60°„µ√°˜OB°‰C°‰£¨µ„G «AC÷–µ„£¨µ„HŒ™÷±œþOC°‰…œ“ª∂ص„£¨µ±°˜GHB°‰Œ™µ»—¸»˝Ω«–Œ ±£¨÷±Ω”–¥≥ˆ∂‘”¶µƒµ„Hµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
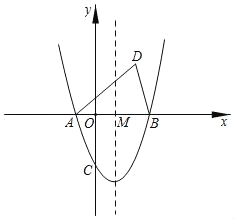
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ωx2+bx+c”Îx÷·Ωª”⁄µ„A£®©Å1£¨0£©°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£®0£¨©Å3£©£Æ
£®1£©«Û≈◊ŒÔœþµƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©“—÷™µ„P£®m£¨n£©‘⁄≈◊ŒÔœþ…œ£¨µ±©Å2°Ðm£º3 ±£¨÷±Ω”–¥nµƒ»°÷µ∑∂Œß£ª
£®3£©≈◊ŒÔœþµƒ∂‘≥∆÷·”Îx÷·Ωª”⁄µ„M£¨µ„D”ε„Cπÿ”⁄µ„M∂‘≥∆£¨ ‘Œ ‘⁄∏√≈◊ŒÔœþ…œ «∑ҥʑ⁄µ„P£¨ π°˜ABP”ΰ˜ABD»´µ»£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆÀ˘”–¬˙◊„Ãıº˛µƒPµ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
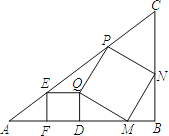
°æƒø°ø»ÁÕº£¨Rt°˜ABC÷–£¨°œB=90°„£¨’˝∑Ω–ŒEFDQ°¢’˝∑Ω–ŒMNPQπ´π≤∂•µ„º«Œ™µ„Q£¨∆‰”ýµƒ∏˜∏ˆ∂•µ„∂º‘⁄Rt°˜ABCµƒ±þ…œ£¨»ÙAC=5£¨BC=3£¨‘ÚEP=____________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø1∫≈ÃΩ≤‚∆¯«Ú¥”∫£∞Œ5m¥¶≥ˆ∑¢£¨“‘1m/minµƒÀŸ∂»…œ…˝.”Î¥ÀÕ¨ ±£¨2∫≈ÃΩ≤‚∆¯«Ú¥”∫£∞Œ15m¥¶≥ˆ∑¢£¨“‘0.5m/minµƒÀŸ∂»…œ…˝.¡Ω∏ˆ∆¯«Ú∂º‘»ÀŸ…œ…˝¡À50min.…Ë∆¯«Ú…œ…˝ ±º‰Œ™x(x°ð0).
(¢Ò)∏˘æð“‚£¨ÃÓ–¥œ¬±Ì
…œ…˝ ±º‰/min | 10 | 30 | °≠ | x |
1∫≈ÃΩ≤‚∆¯«ÚÀ˘‘⁄Œª÷√µƒ∫£∞Œ/m | 15 | °≠ | ||
2∫≈ÃΩ≤‚∆¯«ÚÀ˘‘⁄Œª÷√µƒ∫£∞Œ/m | 30 | °≠ |
(¢Ú)‘⁄ƒ≥ ±øáΩ∏ˆ∆¯«ÚƒÐ∑ÒŒª”⁄Õ¨“ª∏þ∂»£ø»Áπ˚ƒÐ£¨’‚ ±∆¯«Ú…œ…˝¡À∂ý≥§ ±º‰£øŒª”⁄ ≤√¥∏þ∂»£ø»Áπ˚≤ªƒÐ£¨«ÎÀµ√˜¿Ì”….
(¢Û)µ±0°Ðx°Ð50 ±£¨¡Ω∏ˆ∆¯«ÚÀ˘‘⁄Œª÷√µƒ∫£∞Œ◊Ó∂ýœý≤Ó∂ý…Ÿ√◊£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com