

分析 (1)如图(1),设CE=x,则BE=8-x;根据勾股定理列出关于x的方程,解方程即可解决问题.
(2)如图(2),首先求出CB′=3;类比(1)中的解法,设出未知数,列出方程即可解决问题.
解答 解:(1)如图(1),设CE=x,则BE=8-x;
由题意得:AE=BE=8-x,
由勾股定理得:x2+62=(8-x)2,
解得:x=$\frac{7}{4}$,
即CE的长为:$\frac{7}{4}$.
(2)如图(2),
∵点B′落在AC的中点,
∴CB′=$\frac{1}{2}$AC=3;
设CE=x,类比(1)中的解法,可列出方程:x2+32=(8-x)2
解得:x=$\frac{55}{16}$.
即CE的长为:$\frac{55}{16}$.
点评 该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用翻折变换的性质,找出图形中隐含的等量关系;借助勾股定理等几何知识点来分析、判断、推理或解答.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
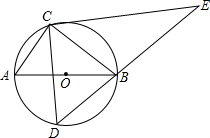 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.
如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
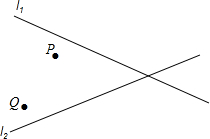 如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).
如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com