
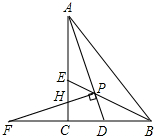
 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H| 1 |
| 2 |
|
|


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
| 5 |
| AC |
| BC |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
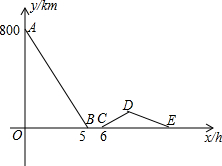 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;查看答案和解析>>
科目:初中数学 来源: 题型:
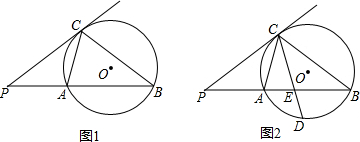
 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com