
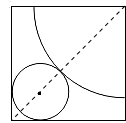
 如图,在边长为23cm的正方形铁皮上,按图示剪取一块圆形和一块扇形铁皮,恰好做成一个圆锥模型,则该圆锥模型的底面半径是________cm.
如图,在边长为23cm的正方形铁皮上,按图示剪取一块圆形和一块扇形铁皮,恰好做成一个圆锥模型,则该圆锥模型的底面半径是________cm. -2
-2 •2πR,求出R=4r.连接OQ、ON,得出正方形OQAN,得出OQ=AQ,根据勾股定理求出AC,AO,即可得出
•2πR,求出R=4r.连接OQ、ON,得出正方形OQAN,得出OQ=AQ,根据勾股定理求出AC,AO,即可得出 r+r+R=23
r+r+R=23 ,求出r即可.
,求出r即可.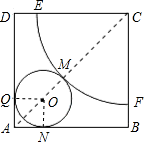
 •2πR,
•2πR,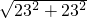 =23
=23 ,
,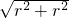 =
= r,
r, r+r+R=23
r+r+R=23 ,
,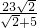 =5
=5 -2.
-2. -2.
-2.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
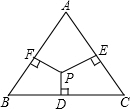 如图所示,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF等于( )
如图所示,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF等于( )A、
| ||
B、2
| ||
C、4
| ||
| D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
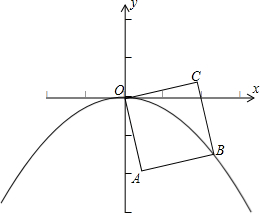 如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )A、-
| ||||
B、-
| ||||
| C、-2 | ||||
D、-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com