
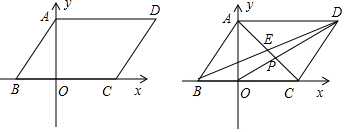
���� ��1�������OA��OB�ij����������OC�����ɵó����ۣ�
��2����������������õ��������ε����ʽ������̼��������M�����ꣻ
��3�����жϳ���POC�ס�PDA�������PC�������PE���ɵó����ۣ�
��� �⣺��1����x2-7x+12=0���ã�x=4��x=3��
��OA��OB��
��OA=4��OB=3��
���ı���ABCD��ƽ���ı��Σ�
��BC=AD=6��
��OC=BC-OB=6-3=3��
��C��3��0����D��6��4����
��2�����ڣ�������������ۣ�
���Ե�AΪ����ʱ��AB=AM��
����Rt��AOB��OA=4��OB=3��
��AB=5��
�ߵ�M��y���ϣ�
��AM=5��
��M��0��9����0��-1����
���Ե�BΪ����ʱ��BM=AB=5��
��M��0��-4����
����ͼ�� �Ե�MΪ����ʱ����AB�Ĵ�ֱƽ���ߣ��ֱ�y�ᣬAB�ڵ�M��F��
�Ե�MΪ����ʱ����AB�Ĵ�ֱƽ���ߣ��ֱ�y�ᣬAB�ڵ�M��F��
�ߡ�AFM=90�㣬
���AFM�ס�AOB��
��$\frac{AF}{AO}=\frac{AM}{AB}$��
��AM=$\frac{25}{8}$��
��M��0��$\frac{7}{8}$����
������0��9����0��-1����0��-4����0��$\frac{7}{8}$����
��3����Rt��AOC��OA=4��OC=3��
��AC=5��
��AD��OC��
���POC�ס�PDA��
��$\frac{PC}{AP}=\frac{OC}{AD}$=$\frac{3}{6}$=$\frac{1}{2}$��
��$\frac{PC}{AC}=\frac{1}{3}$��
��PC=$\frac{5}{3}$��
���ı���ABCD��ƽ���ı��Σ�
��CE=$\frac{1}{2}$AC=$\frac{5}{2}$��
��PE=$\frac{5}{6}$��
��PE��PC=$\frac{5}{6}$��$\frac{5}{3}$=1��2��
���� �������������ۺ��⣬��Ҫ������ƽ���ı��ε����ʣ���һԪ���η��̣����������ε����ʣ�ƽ���ı��ε����ʣ��Ȿ��Ĺؼ����÷��̵�˼��˼�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
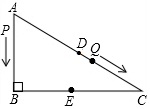 ��ͼ����Rt��ABC�У���B=90�㣬��C=30�㣬AB=12���ף���P��A��������·AB-BC�������˶�����Q��AC���е�Dͬʱ��������·DC-CB�������˶�������P��������P��Q���ٶȷֱ�Ϊ1����/�롢a����/�루a��1����������t�����BC���ϵ�ijһ��E������
��ͼ����Rt��ABC�У���B=90�㣬��C=30�㣬AB=12���ף���P��A��������·AB-BC�������˶�����Q��AC���е�Dͬʱ��������·DC-CB�������˶�������P��������P��Q���ٶȷֱ�Ϊ1����/�롢a����/�루a��1����������t�����BC���ϵ�ijһ��E������ �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
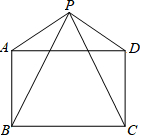 ��ͼ���ı���ABCD�У�AD=BC��P���ı���ABCD��һ�㣬��PA=PD��PB=PC����APB=��DPC��
��ͼ���ı���ABCD�У�AD=BC��P���ı���ABCD��һ�㣬��PA=PD��PB=PC����APB=��DPC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
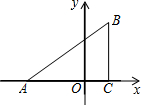 ��֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB=90�㣬��A��C������ֱ�ΪA��-3��0����C��1��0����$\frac{BC}{AC}$=$\frac{3}{4}$��
��֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB=90�㣬��A��C������ֱ�ΪA��-3��0����C��1��0����$\frac{BC}{AC}$=$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com