
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
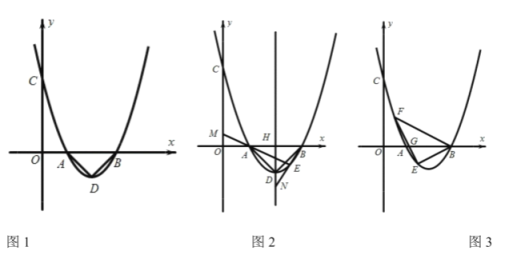
(1)如图1,请求出![]() 三点的坐标;
三点的坐标;
(2)点![]() 为
为![]() 轴下方抛物线
轴下方抛物线![]() 上一动点.
上一动点.
①如图2,若![]() 时,抛物线的对称轴
时,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交对称轴
交对称轴![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
②如图3,若![]() 时,点
时,点![]() 在
在![]() 轴上方的抛物线上运动,连接
轴上方的抛物线上运动,连接![]() 交
交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() 当线段
当线段![]() 运动时,
运动时,![]() 的度数大小发生变化吗?若不变,请求出
的度数大小发生变化吗?若不变,请求出![]() 的值若变化,请说明理由.
的值若变化,请说明理由.
【答案】(1)![]() ;(2)①2; ②
;(2)①2; ②![]() =4,理由见解析
=4,理由见解析
【解析】
(1)令y=0,代入函数解析式,令x=0,代入函数解析式,即可求解;
(2)①过点![]() 作
作![]() 轴于点
轴于点![]() ,设点
,设点![]() ,由
,由![]() ,
,![]() ,得
,得![]() ,从而得
,从而得![]() ,进而即可得到结论;②设点
,进而即可得到结论;②设点![]() ,由题意得:
,由题意得:![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,由
,由![]() ,得
,得![]() ,从而得
,从而得![]() ,结合正切三角函数的定义,即可得到结论.
,结合正切三角函数的定义,即可得到结论.
(1)令y=0代入![]() ,得
,得![]() ,
,
解得:![]() ,
,
令x=0代入![]() ,得:y=3k,
,得:y=3k,
∴![]() ;
;
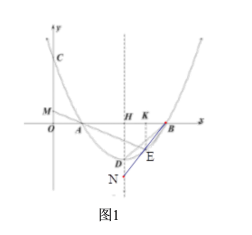
(2)①过点![]() 作
作![]() 轴于点
轴于点![]() ,如图1,则
,如图1,则![]() ,
,![]() ,
,
∵当![]() 时,
时,![]() ,对称轴为:直线x=2,
,对称轴为:直线x=2,
∴设点![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ;
;
②不会变化,理由如下:
∵当![]() 时,
时,![]() ,
,
∴设点![]() ,
,
∵当![]() 时,不能满足
时,不能满足![]() ,
,
![]() ,
,
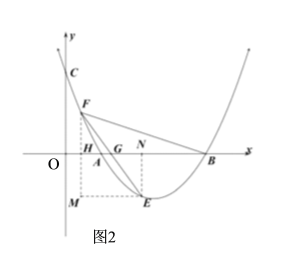
如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() ,∠FHB=∠ENB=90°,
,∠FHB=∠ENB=90°,
![]() ,
,
![]() ,
,
![]() ,
,
∵EM∥x轴,
∴∠FGO=∠FEM,
![]()
∴点![]() 和点
和点![]() 在抛物线上运动时,
在抛物线上运动时,![]() 的值不会变化.
的值不会变化.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知AB=AC.如图,D、E为∠BAC的平分线上的两点,连接BD、CD、BE、CE;如图4, D、E、F为∠BAC的平分线上的三点,连接BD、CD、BE、CE、BF、CF;如图5, D、E、F、G为∠BAC的平分线上的四点,连接BD、CD、BE、CE、BF、CF、BG、CG……依此规律,第17个图形中有全等三角形的对数是( )

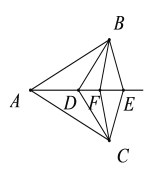

A.17B.54C.153D.171
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=a![]() -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).
(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-![]() a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.
①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
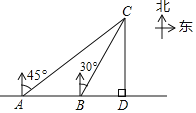
【题目】今年“五一”期间,小明一家到某农庄采摘,在村口A处,小明接到农庄发来的定位,发现农庄C在自己的北偏东45°方向,于是沿河边笔直绿道l步行200米到达B处,此时定位显示农庄C在自己的北偏东30°方向,电话联系,得知农庄主已到农庄C正南方的桥头D处等待,请问还要沿绿道直走多少米才能到达桥头D处.(精确到1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
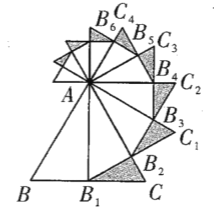
【题目】如图,已知等边![]() 的边长是
的边长是![]() ,以
,以![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边![]() ;再以等边
;再以等边![]() 的
的![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边![]() ,再以等边
,再以等边![]() 的
的![]() 边上的高
边上的高![]() 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边![]() : ....记
: ....记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,如此下去,则
,如此下去,则![]() ___________
___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙三人做一个抽牌游戏,三张纸牌上分别写有个数字0,x,y(x,y均为正整数,且x<y),每人抽一张纸牌,纸牌上的数字就是这一轮的得分.经过若干轮后(至少四轮),甲的总得分为20,乙的总得分为10,丙的总得分为9.则甲抽到x的次数最多为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
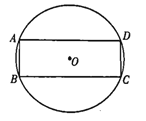
【题目】如图,⊙O为短形ABCD的外接圆,其半径为3.
(1)用尺规作图作出∠ABC的平分线,并标出它与劣弧AD的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦AD的距离为2,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
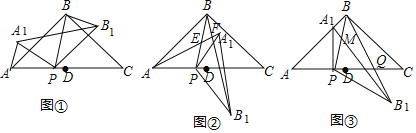
【题目】在△ABC中,AB=BC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A、点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB1.
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=![]() ,设AP=x,CQ=y,求y关于x的函数关系式.
,设AP=x,CQ=y,求y关于x的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com