
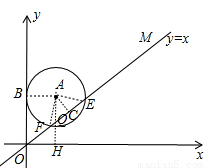
(本题满分12分)如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,﹣2).直线OM是一次函数y=x的图像.让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
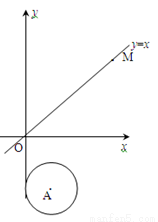
(1)填空
①直线OM与x轴所夹的锐角度数为 °;
②当t= 时,⊙A与坐标轴有两个公共点;
(2)当t>3时,求出运动过程中⊙A与直线OM相切时的t的值;
(3)运动过程中,当⊙A与直线OM相交所得的弦长为1时,求t的值.
(1)①45°;②t=1或2或3时⊙A与坐标轴有两个交点;
(2)t=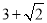 ;(3)t=
;(3)t=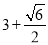 或t=
或t=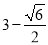 .
.
【解析】
试题解析:【解析】
(1)①直线OM与x轴所夹的锐角度数是45°;
②当点A的坐标是(1,-1)时⊙A与坐标轴有两个交点,此时t=1;
当点A的坐标是(1,0)时⊙A与坐标轴有两个交点,此时t=2;
当点A的坐标是(1,1)时⊙A与坐标轴有两个交点,此时t=3;
所以t=1或2或3时⊙A与坐标轴有两个交点;
(2)如下图所示,当t=3时,点A的坐标是(1,1),
⊙A与直线OM相交,
所以当t>3时,⊙A在直线OM上方,
如果⊙A相切,
则AB=1,
因为直线OM与x轴的夹角是45°,
所以∠ACB=45°,
点C的坐标是(1,1),
所以BC=1,
则有AC=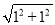 =
=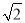 ,
,
所以运动的时间是t=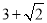 ;
;
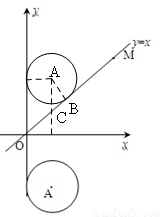
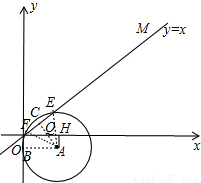
(3)如下图所示,当点A在x轴下方时,
过点A作AB⊥y轴于B,AC⊥OM于C,交x轴于点Q,AH⊥x轴于点H,
⊙A与直线OM交于E、F,
则AB=OH=1,AE=AF=1,OB=AH=2-t,
∵EF=1,
∴△AEF是等边三角形,
∴AC=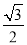 AE=
AE=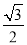 ,
,
∵直线OM与x轴的夹角是45°,
∴△OCQ与△AHQ都是等腰直角三角形,
∴HQ=AH=2-t,
∴OQ=OH-HQ=t-1,AQ=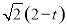 ,
,
∴CQ= OQ=
OQ=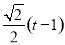 ,
,
∵AC=CQ+AQ,
∴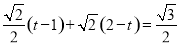 ,
,
∴t=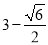 ;
;
当点A在x轴上方时,如下图所示,过点A作AB⊥y轴于B,AC⊥OM于C,
过点A作 AH⊥x轴于点H,交直线OM于点Q,
⊙A与直线OM交于E、F,
则AB=OH=1,AE=AF=1,OB=AH=2-t,
∵EF=1,
∴△AEF是等边三角形,
∴AC=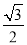 ,
,
∵直线OM与x轴的夹角是45°,
∴△OCQ与△AHQ都是等腰直角三角形,
∴HQ=OH=1,
AQ=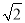 AC=
AC=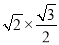 =
= ,
,
∵AH=HQ+AQ,
∴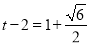 ,
,
∴t=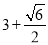
∴t=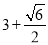 或t=
或t=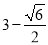 .
.
考点:圆的综合题
点评:本题主要考查了切线的性质、垂径定理、等边三角形的判定与性质、等腰直角三角形的判定与性质,本题难度较大综合性较强,在解决本题时应注意分类讨论.


科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(解析版) 题型:填空题
已知抛物线的顶点坐标为(﹣1,﹣2),且通过点(1,10),则该抛物线的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质1(解析版) 题型:?????
同学们在一起探讨研究下面的题目:
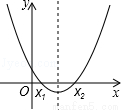
函数y=x2﹣x+m(m为常数)的图象如图所示,
如果x=a时,y<0;那么x=a﹣1时,函数值为( )
甲同学说:我注意到当x=0时,y=m>0.
乙同学说:我发现函数图象的对称轴为x=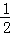 .
.
丙同学说:我判断出x1<a<x2.
丁同学说:我认为关键要判断a﹣1的符号.
参考上面同学们的讨论,你认为该题应选择的答案是( )
A.y<0 B.0<y<m C.y>m D.y=m
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古赤峰市宁城县九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
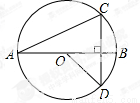
A.160° B.150° C.140° D.120°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分8分)如图,△ABC是⊙O的内接三角形,直径AD=8,∠ABC=∠DAC.

(1)求AC的长;
(2)求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏如皋市港城实验学校九年级上学期期中调研数学试卷 (解析版) 题型:解答题
(本题满分12分)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数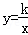 (k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.
(k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.
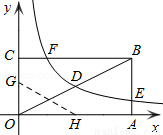
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安地区八年级上学期期末模拟数学试卷(解析版) 题型:选择题
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为( )
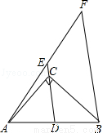
A.6 B.7 C.8 D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com