
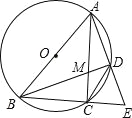
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.
(1)求证:BCCE=ACMC;
(2)若点D是劣弧AC的中点,tan∠ACD=![]() ,MDBD=10,求⊙O的半径.
,MDBD=10,求⊙O的半径.
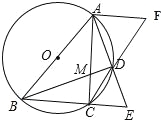
(3)若CD∥AB,过点A作AF∥BC,交CD的延长线于点F,求![]() ﹣
﹣![]() 的值.
的值.
【答案】(1)见试题解析;(2)5;(3)1.
【解析】
试题分析:(1)要证明BCCE=ACMC,即证明![]() =
=![]() ,即证明△CBM∽△CAE;
,即证明△CBM∽△CAE;
(2)因为点D是劣弧![]() 的中点,所以
的中点,所以![]() =
=![]() ,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MDBD=10,再由tan∠ACD=tan∠ABD=
,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MDBD=10,再由tan∠ACD=tan∠ABD=![]() ,求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
,求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
(3)因为CD∥AB,AF∥BC,所以△CDE∽△BAE,△ADF∽△DEC,利用对边的比相等可得![]() =
=![]() ,所以
,所以![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() .
.
试题解析:(1)∵![]() =
=![]() ,∴∠MBC=∠CAE,∵AB是⊙O的直径,∴∠BCM=∠ACE=90°,∴△CBM∽△CAE,∴
,∴∠MBC=∠CAE,∵AB是⊙O的直径,∴∠BCM=∠ACE=90°,∴△CBM∽△CAE,∴![]() =
=![]() ,∴BCCE=ACMC;
,∴BCCE=ACMC;
(2)∵点D是劣弧![]() 的中点,∴
的中点,∴![]() =
=![]() ;∴∠ABD=∠MBC,∠ACD=∠CAE,∵∠MBC=∠CAE,
;∴∠ABD=∠MBC,∠ACD=∠CAE,∵∠MBC=∠CAE,
∴∠ABD=∠CAE=∠ACD,∵AB是⊙O的直径,∴∠ADB=90°,∴△AMD∽△BAD,
∴![]() =
=![]() ,∴AD2=MDBD=10,∴AD=
,∴AD2=MDBD=10,∴AD=![]() ,∵tan∠ACD=tan∠ABD=
,∵tan∠ACD=tan∠ABD=![]() ,∴
,∴![]() ,
,
∴BD=3![]() ,∵AB2=AD2+BD2,∴AB=
,∵AB2=AD2+BD2,∴AB=![]() =10,∴⊙O的半径为:
=10,∴⊙O的半径为:![]() AB=5;
AB=5;
(3)∵CD∥AB,∴△CDE∽△BAE,∴![]() =
=![]() ,∵AF∥CE,∴△ADF∽△DEC,
,∵AF∥CE,∴△ADF∽△DEC,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() =1.
=1.


科目:初中数学 来源: 题型:
【题目】小明去超市买东西花20元,他身上只带了面值为2元和5元的纸币,营业员没有零钱找给他,那么小明付款有几种方式( )
A.2种
B.3种
C.4种
D.5种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是______元;②月销量是______件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A.一个三角形中至少有两个锐角
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.同角的余角相等
D.一个角的补角大于这个角本身
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒子里有若干个大小相同的白球和红球,从中任意摸出一个球,摸到红球得2分,摸到白球得3分.某人摸到x个红球,y个白球,共得12分.列出关于x、y的二元一次方程:
查看答案和解析>>
科目:初中数学 来源: 题型:
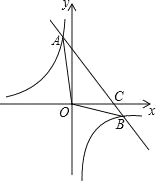
【题目】如图,已知一次函数y=ax+b的图象与反比例函数y=![]() 的图象相交于点A(﹣2,m)和点B(4,﹣2),与x轴交于点C
的图象相交于点A(﹣2,m)和点B(4,﹣2),与x轴交于点C
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
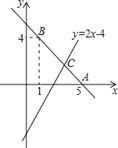
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种商品按进货价提高100%后,又以6折优惠售出,售价为60元,则这种商品的进货价是( )
A. 120元 B. 100元 C. 72元 D. 50元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com