
【题目】等腰直角△ABC中,BC=AC,∠ACB=90°,将该三角形在直角坐标系中放置.

(1)如图(1),过点A作AD⊥x轴,当B点为(0,1),C点为(3,0)时,求OD的长;
(2)如图(2),将斜边顶点A、B分别落在y轴上、x轴上,若A点为(0,1),B点为(4,0),求C点坐标;
【答案】(1)4;(2)(![]() )
)
【解析】
(1)通过证明△BOC≌△CDA,可得CD=OB=1,即可求OD的长;
(2)过点C作CF⊥y轴,CE⊥x轴,通过证明△ACF≌△BCE,可得BE=AF,CF=CE,可证四边形CEOF是正方形,可得CF=OE=OF=CE,即可求点C坐标.
解:(1)∵B点为(0,1),C点为(3,0)
∴OB=1,OC=3
∵∠ACB=90°,
∴∠BCO+∠ACD=90°,且∠BCO+∠OBC=90°
∴∠ACD=∠OBC,且AC=BC,∠BOC=∠ADC=90°,
∴△BOC≌△CDA(AAS)
∴CD=OB=1
∴OD=OC+CD=4
(2)如图,过点C作CF⊥y轴,CE⊥x轴,
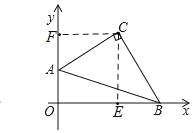
∵A点为(0,1),B点为(4,0),
∴AO=1,BO=4
∵CF⊥y轴,CE⊥x轴,∠AOB=90°,
∴四边形CEOF是矩形,
∴∠ECF=90°,
∴∠FCA+∠ACE=90°,且∠ACE+∠BCE=90°,
∴∠FCA=∠BCE,且AC=BC,∠CFA=∠CEB=90°,
∴△ACF≌△BCE(AAS)
∴BE=AF,CF=CE,
∴矩形CEOF是正方形
∴CF=OE=OF=CE,
∴OA+AF=OB﹣BE
∴2AF=OB﹣OA
∴AF=![]()
∴OF=![]()
∴点C(![]() ,
,![]() )
)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边长分别为m+2,m+4.(其中m为正整数)


(1) 图①中长方形的面积![]() =_______________
=_______________
图②中长方形的面积![]() =_______________
=_______________
比较:![]() ______
______![]() (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2) 现有一正方形,其周长与图①中的长方形周长相等,
①求正方形的边长(用含m的代数式表示);
②试说明:该正方形面积![]() 与图①中长方形面积
与图①中长方形面积![]() 的差(即
的差(即![]() -
-![]() )是定值.
)是定值.
(3) 在(1)的条件下,若某个图形的面积介于![]() 、
、![]() 之间(不包括
之间(不包括![]() 、
、![]() )并且面积为整数,这样的整数值有且只有20个,求m的值.
)并且面积为整数,这样的整数值有且只有20个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2-6ax+4a+3的图像与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.
(1)则点A的坐标为 , a=;
(2)过点A作AB的垂线与该二次函数的图像交于另一点C,求点C的坐标;
(3)连接BC,过点A作直线l交线段BC于点P,设点B、点C到l的距离分别为d1、d2 , 求d1+d2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,AB∥CD,E为直线CD下方一点,BF平分∠ABE.

(1)求证:∠ABE+∠C﹣∠E=180°.
(2)如图2,EG平分∠BEC,过点B作BH∥GE,求∠FBH与∠C之间的数量关系.
(3)如图3,CN平分∠ECD,若BF的反向延长线和CN的反向延长线交于点M,且∠E+∠M=130°,请直接写出∠E的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6交x轴于A,交y轴于B.

(1)直接写出A( , ),B( , );
(2)如图1,点E为直线y=x+2上一点,点F为直线y=![]() x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
(3)如图2,点C(m,n)为线段AB上一动点,D(﹣7m,0)在x轴上,连接CD,点M为CD的中点,求点M的纵坐标y和横坐标x之间的函数关系式,并直接写出在点C移动过程中点M的运动路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M在线段BC上,点E和N在线段AC上,EM∥AB,BE和MN分别平分∠ABC和∠EMC.下列结论:①∠MBN=∠MNB;②∠MBE=∠MEB;③MN∥BE.其中正确的是( )

A.①②③B.②③C.①③D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0.

(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠A=30°.
(1)用直尺和圆规作AB的垂直平分线,分别交AC、AB于点E.D(保留作图痕迹,不写作法)
(2)猜想AC与CE之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下(单位:分):
A班:88,91,92,93,93,93,94,98,98,100
B班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
A班 | 100 | a | 93 | 93 | c |
B班 | 99 | 95 | b | 93 | 8.4 |
(1)求表中a、b、c的值;
(2)依据数据分析表,有人说:“最高分在A班,A班的成绩比B班好”,但也有人说B班的成绩要好,请给出两条支持B班成绩好的理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com