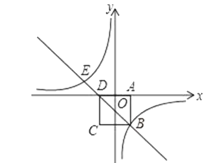
【题目】如图，在平面直角坐标系中，边长为 2 的正方形 ABCD 关于 y 轴对称，边 AD 在 x 轴上，点 B 在第四象限，直线 BD与反比例函数 y=
的图象交于 B、E 两点.
（1）求反比例函数的解析式；
（2）求点 E 的坐标
.
【答案】（1）
；（2）点E的坐标为（-2,1）.
【解析】
（1）根据正方形的边长，正方形关于y轴对称，可得点A、B、D的坐标，根据待定系数法，可得函数解析式；
（2）根据两个函数解析式，组成方程组，解方程组，即可得答案．
解：（1）∵边长为2的正方形ABCD关于y轴对称，边AD在x轴上，点B在第四象限，
∴A（1,0），D（-1,0），B（1，-2）.
∵反比例函数
的图象经过点B，
∴m=1
（-2）=-2.
∴反比例函数解析式为
.
（2）设直线BD的解析式为
，
∴
，
解得
.
∴直线BD的解析式为：
∵直线BD与反比例函数的图象交于B、E两点，
∴
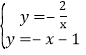
解得
或
∵B（1，-2）.
∴点E的坐标为（-2,1）.
名师点拨卷系列答案
英才计划期末调研系列答案科目：初中数学 来源： 题型：
【题目】已知:点
在
上,弦
,垂足
,弦
,垂足为
,弦
与
相交于点
；
(1)如图
,求证:
；
(2)如图
,连接
,当平分
时,求证:弧
弧
；
(3)如图
,在(2)的条件下,半径与相交于点
,连接
,若
,求线段
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
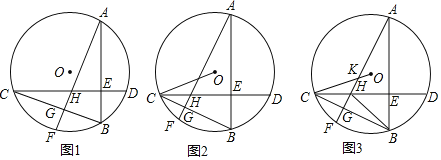
【题目】已知二次函数
图象的一部分如图所示，给出以下结论：
；
当
时，函数有最大值；
方程
的解是
，
；
，其中结论错误的个数是
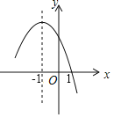
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
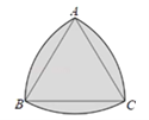
【题目】如图，分别以等边三角形 ABC 的三个顶点为圆心，以边长为半径画弧，得到的封闭图形就是“勒洛三角形”（勒洛 三角形是定宽曲线所能构成的面积最小的图形)，若 AB=2，则勒洛三角形的面积为( )
A. π+ 
B. π-C. 2π+2 D. 2π-2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个，某学习小组进行摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再放回，下表是活动进行中的一组统计数据：
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
当n很大时，估计从袋中摸出一个黑球的概率是______；
试估算口袋中白球有______个；
在的条件下，若从中先换出一球，不放回，摇匀后再摸出一球，请用列表或树状图的方法求两次都摸到白球的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市某楼盘准备以每平方米15000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米12150元的均价开盘销售
求平均每次下调的百分率．
某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：
打
折销售；
不打折，一次性送装修费每平方米250元．
试问哪种方案更优惠？比另外一种方案优惠多少元？
不考虑其他因素
查看答案和解析>>
科目：初中数学 来源： 题型：
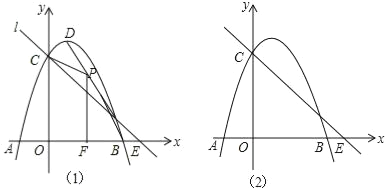
【题目】如图1，抛物线y=﹣x2+2x+3与x轴交于A，B，与y轴交于C，抛物线的顶点为D，直线l过C交x轴于E（4，0）．
（1）写出D的坐标和直线l的解析式；
（2）P（x，y）是线段BD上的动点（不与B，D重合），PF⊥x轴于F，设四边形OFPC的面积为S，求S与x之间的函数关系式，并求S的最大值；
（3）点Q在x轴的正半轴上运动，过Q作y轴的平行线，交直线l于M，交抛物线于N，连接CN，将△CMN沿CN翻转，M的对应点为M′．在图2中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对任意一个四位数n，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n为“极数”，记为n=
其中
，且x、y为整数
请任意写出两个“极数”；
猜想任意一个“极数”是否是99的倍数，请说明理由；
如果一个正整数a是另一个正整数b的平方，则称正整数a是完全平方数，若四位数m为“极数”，记
写出三个满足
是完全平方数的
只需直接写出结果．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
