
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.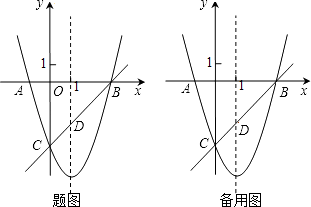
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ= ![]() AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.
【答案】
(1)
解:∵抛物线的对称轴为直线x=1,
∴ ![]()
∴b=﹣2
∵抛物线与y轴交于点C(0,﹣3),
∴c=﹣3,
∴抛物线的函数表达式为y=x2﹣2x﹣3;
(2)
解:∵抛物线与x轴交于A、B两点,
当y=0时,x2﹣2x﹣3=0.
∴x1=﹣1,x2=3.
∵A点在B点左侧,
∴A(﹣1,0),B(3,0)
设过点B(3,0)、C(0,﹣3)的直线的函数表达式为y=kx+m,
则 ![]() ,∴
,∴ ![]()
∴直线BC的函数表达式为y=x﹣3;
(3)
解:
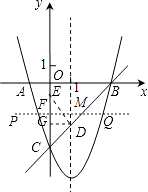
①∵AB=4,PQ= ![]() AB,
AB,
∴PQ=3
∵PQ⊥y轴
∴PQ∥x轴,
则由抛物线的对称性可得PM= ![]() ,
,
∵对称轴是直线x=1,
∴P到y轴的距离是 ![]() ,
,
∴点P的横坐标为 ![]() ,
,
∴P( ![]() ,
, ![]() )
)
∴F(0, ![]() ),
),
∴FC=3﹣OF=3﹣ ![]() =
= ![]()
∵PQ垂直平分CE于点F,
∴CE=2FC= ![]()
∵点D在直线BC上,
∴当x=1时,y=﹣2,则D(1,﹣2),
过点D作DG⊥CE于点G,
∴DG=1,CG=1,
∴GE=CE﹣CG= ![]() ﹣1=
﹣1= ![]() .
.
在Rt△EGD中,tan∠CED= ![]() .
.
②P1(1﹣ ![]() ,﹣2),P2(1﹣
,﹣2),P2(1﹣ ![]() ,﹣
,﹣ ![]() ).
).
设OE=a,则GE=2﹣a,
当CE为斜边时,则DG2=CGGE,即1=(OC﹣OG)(2﹣a),
∴1=1×(2﹣a),
∴a=1,
∴CE=2,
∴OF=OE+EF=2
∴F、P的纵坐标为﹣2,
把y=﹣2,代入抛物线的函数表达式为y=x2﹣2x﹣3得:x=1+ ![]() 或1﹣
或1﹣ ![]()
∵点P在第三象限.
∴P1(1﹣ ![]() ,﹣2),
,﹣2),
当CD为斜边时,DE⊥CE,
∴OE=2,CE=1,
∴OF=2.5,
∴P和F的纵坐标为:﹣ ![]() ,
,
把y=﹣ ![]() ,代入抛物线的函数表达式为y=x2﹣2x﹣3得:x=1﹣
,代入抛物线的函数表达式为y=x2﹣2x﹣3得:x=1﹣ ![]() ,或1+
,或1+ ![]() ,
,
∵点P在第三象限.
∴P2(1﹣ ![]() ,﹣
,﹣ ![]() ).
).
综上所述:满足条件为P1(1﹣ ![]() ,﹣2),P2(1﹣
,﹣2),P2(1﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】已知C点的坐标,即知道OC的长,可在直角三角形BOC中根据∠BCO的正切值求出OB的长,即可得出B点的坐标.已知了△AOC和△BOC的面积比,由于两三角形的高相等,因此面积比就是AO与OB的比.由此可求出OA的长,也就求出了A点的坐标,然后根据A、B、C三点的坐标即可用待定系数法求出抛物线的解析式.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
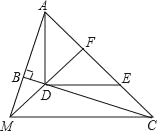
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
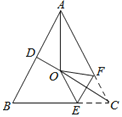
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图,并回答问题:
如图,在同一平面内有三点A,B,C.

(1)画直线AC;
(2)画射线CB;
(3)过点B作直线AC的垂线BD,垂足为D;
(4)画线段AB及线段AB的中点E,连接DE;
(5)通过画图和测量,与线段DE长度相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:

(1)FC=AD;
(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,∠A=30°,AB=4. 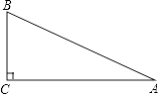
(1)作AC边上的垂直平分线DE,交AC于点D,交AB于点E(用尺规作图法,保留作图痕迹,不要求写作法和证明):
(2)连接CE,求△BEC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
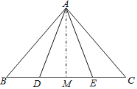
【题目】已知点![]() 、
、![]() 在
在![]() 的
的![]() 边上,
边上,![]() ,
,![]() ,为了判断
,为了判断![]() 与
与![]() 的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
解:作![]() ,垂足为
,垂足为![]()
∵![]() ,
,
∴![]() 是________三角形,
是________三角形,
∴![]() ________
________
又∵![]() ,
,
∴![]() ________,即
________,即![]() ________;
________;
又∵________(自己所作),
∴![]() 是线段________的垂直平分线;
是线段________的垂直平分线;
∴![]() ________
________
∴________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com