
【题目】如图,![]() 的四个内角的平分线分别相交于点
的四个内角的平分线分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() ,四边形
,四边形![]() 是怎样的特殊四边形?证明你的结论.
是怎样的特殊四边形?证明你的结论.

【答案】矩形,证明见解析
【解析】
由于四边形ABCD是平行四边形,那么AB∥CD,利用平行线的性质可得∠ABC+∠BCD=180°,而BH,CH分别平分∠ABC与∠BCD,则∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
四边形EFGH是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,
∠BCD,
∴∠HBC+∠HCB=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.


科目:初中数学 来源: 题型:
【题目】某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.
(1)求购买甲、乙两种树苗各多少棵?
(2)为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣1)23×(π﹣3)0﹣(﹣![]() ) ﹣3;
) ﹣3;
(2)aa2a3+(﹣2a3)2﹣a8÷a2;
(3)(x+4)2﹣(x+2)(x﹣2);
(4)(a+2b﹣3c)(a﹣2b+3c).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,将一块等腰直角三角形的直角顶点放在斜边
,将一块等腰直角三角形的直角顶点放在斜边![]() 的中点
的中点![]() 处,将三角板绕点
处,将三角板绕点![]() 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
(1)观察图①,当三角板绕点![]() 旋转到
旋转到![]() 时,我们发现:
时,我们发现:![]() __________
__________![]() .(选填“
.(选填“![]() ”、“
”、“![]() ”或“
”或“![]() ”)
”)
(2)当三角板绕点![]() 旋转到图②所示位置时,判断(1)题中
旋转到图②所示位置时,判断(1)题中![]() 与
与![]() 之间的大小关系还存在吗?请你结合图②说明理由.
之间的大小关系还存在吗?请你结合图②说明理由.
(3)三角板绕点![]() 旋转,
旋转,![]() 是否能成为等腰三角形?若能,指出所有情况(那写出
是否能成为等腰三角形?若能,指出所有情况(那写出![]() 为等腰三角形时
为等腰三角形时![]() 的长);若不能,请说明理由.
的长);若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D,求证:∠B=∠C.

请在下面的证明过程的括号内,填写依据.
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD( )
∵∠1+∠2=180°(已知)
∴∠2+∠CGD=180°(等量代换)
∴AE//FD( )
∴∠AEC=∠D( )
∵∠A=∠D(已知)
∴∠AEC=∠A( )
∴AB//CD( )
∴∠B=∠C( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
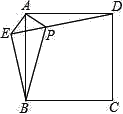
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com