
根据二次函数y=ax2+bx+c(a≠0,a、b、c为常数)得到一些对应值,列表如下:
|
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
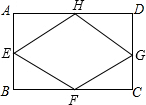 (2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一元二次方程x2+ax+a-2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根;
(2)设a<0,当二次函数y=x2+ax+a-2的图象与x轴的两个交点的距离为![]() 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为![]() ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.
【解析】(1)判断上述方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了,(2)根据二次函数图象与x轴的两个交点的距离公式解答即可.(3)是二次函数综合应用问题和三角形的综合应用
查看答案和解析>>
科目:初中数学 来源:2013届黑龙江省哈尔滨市松北区九年级升学调研测试(一)数学试卷(带解析) 题型:解答题
已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.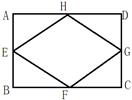
(1)请直接写出y与x的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.
(参考公式:当x=- 时,二次函数y=ax+bx+c(a≠o)有最小(大)值
时,二次函数y=ax+bx+c(a≠o)有最小(大)值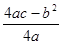 )
)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年黑龙江省哈尔滨市松北区九年级升学调研测试(一)数学试卷(解析版) 题型:解答题
已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.

(1)请直接写出y与x的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.
(参考公式:当x=- 时,二次函数y=ax+bx+c(a≠o)有最小(大)值
时,二次函数y=ax+bx+c(a≠o)有最小(大)值 )
)
查看答案和解析>>
科目:初中数学 来源:2012届北京市西城区九年级一模数学卷(解析版) 题型:解答题
已知一元二次方程x2+ax+a-2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根;
(2)设a<0,当二次函数y=x2+ax+a-2的图象与x轴的两个交点的距离为 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为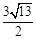 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.
【解析】(1)判断上述方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了,(2)根据二次函数图象与x轴的两个交点的距离公式解答即可.(3)是二次函数综合应用问题和三角形的综合应用
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com