
 12、如图△ABC≌DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD②∠DAC+∠DBC=180°③△ADC∽△BEC④CD⊥AB,其中成立的是( )
12、如图△ABC≌DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD②∠DAC+∠DBC=180°③△ADC∽△BEC④CD⊥AB,其中成立的是( )

 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
 10、如图,△DEC是由△ABC经过了如下的几何变换而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转90°得△A′B′C′,再以A′C′所在直线为对称轴作轴对称;③将△ABC向下向左各平移1个单位,再以AC的中点为中心作中心对称,其中正确的变换有( )
10、如图,△DEC是由△ABC经过了如下的几何变换而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转90°得△A′B′C′,再以A′C′所在直线为对称轴作轴对称;③将△ABC向下向左各平移1个单位,再以AC的中点为中心作中心对称,其中正确的变换有( )查看答案和解析>>
科目:初中数学 来源: 题型:单选题
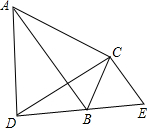 如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是
如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市中考数学模拟试卷(3)(解析版) 题型:选择题
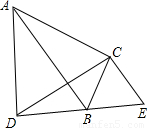
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com