Question

6．如图，点A为y轴正半轴上一点，点B是A关于x轴的对称点，过点A任意作一条直线，与抛物线y=$\frac{3}{4}$x²交于P，Q两点．

（1）如图1，若PQ∥x轴，点A坐标为（0，3），求证：∠ABP=∠ABQ
（2）若直线绕点A旋转到图2的位置，问：题（1）中的结论是否依然成立，请说明理由．

Answer 1

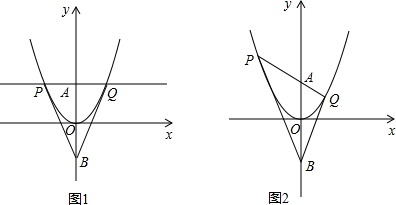
分析 （1）由PQ∥x轴以及点A的坐标，可将y=3代入抛物线解析式中求出点P、Q的坐标，由此可得出PA=QA，再由∠PAB=∠QAB=90°以及两三角形有公共边AB可证出△PAB≌△QAB，由全等三角形的性质即可得出结论；
（2）结论成立．分别过点P，Q作y轴的垂线，垂足分别为C，D，设点A的坐标为（0，t），则点B的坐标为（0，-t）．设直线PQ的函数解析式为y=kx+t，并设P，Q的坐标分别为（x_P，y_P），（x_Q，y_Q）．将一次函数解析式代入二次函数解析式中可得出关于x的一元二次方程，利用根与系数的关系、二次函数图象上点的坐标特征以及相似三角形的判定定理即可得出△BCP∽△BDQ，从而得出∠ABP=∠ABQ．

解答 （1）证明：∵PQ∥x轴，点A坐标为（0，3），
∴点P，点Q的纵坐标均为3．
令y=$\frac{3}{4}$x²中y=3，则有$\frac{3}{4}$x²=3，
解得：x=±2，
∴点P的坐标为（-2，3），点Q的坐标为（2，3），
∴PA=QA．
∵PQ∥x轴，y轴⊥x轴，
∴PQ⊥y轴，
∴∠PAB=∠QAB=90°．
在△PAB和△QAB中，有$\left\{\begin{array}{l}{PA=QA}\\{∠PAB=∠QAB}\\{AB=AB}\end{array}\right.$，
∴△PAB≌△QAB（SAS），
∴∠ABP=∠ABQ．
（2）解：题（1）中的结论依然成立．理由如下：
如图，分别过点P，Q作y轴的垂线，垂足分别为C，D．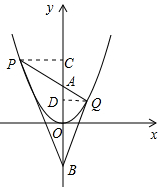
设点A的坐标为（0，t），则点B的坐标为（0，-t）．
设直线PQ的函数解析式为y=kx+t，并设P，Q的坐标分别为（x_P，y_P），（x_Q，y_Q）．
将y=kx+t代入y=$\frac{3}{4}$x²，整理得：
$\frac{3}{4}$x²-kx-t=0．
∴x_P•x_Q=-$\frac{4}{3}$t，即t=-$\frac{3}{4}$x_P•x_Q，
∴$\frac{BC}{BD}$=$\frac{{y}_{P}+t}{{y}_{Q}+t}$=$\frac{\frac{3}{4}{{x}_{P}}^{2}+t}{\frac{3}{4}{{x}_{Q}}^{2}+t}$=$\frac{\frac{3}{4}{{x}_{P}}^{2}-\frac{3}{4}{x}_{P}•{x}_{Q}}{\frac{3}{4}{{x}_{Q}}^{2}-\frac{3}{4}{x}_{P}•{x}_{Q}}$=$\frac{\frac{3}{4}{x}_{P}•（{x}_{P}-{x}_{Q}）}{\frac{3}{4}{x}_{Q}•（{x}_{Q}-{x}_{P}）}$=-$\frac{{x}_{P}}{{x}_{Q}}$．
又∵$\frac{PC}{QD}$=-$\frac{{x}_{P}}{{x}_{Q}}$，
∴$\frac{BC}{BD}$=$\frac{PC}{QD}$．
又∵∠BCP=∠BDQ=90°，
∴△BCP∽△BDQ，
∴∠ABP=∠ABQ．

点评 本题考查了全等三角形的判定及性质、二次函数图象上点的坐标特征、根与系数的关系以及相似三角形的判定与性质，解题的关键是：（1）证出△PAB≌△QAB；（2）找出△BCP∽△BDQ．本题属于中档题，难度不大，解决该题型题目时，根据边角关系结合全等（相似）三角形的判定定理证出两三角形全等（相似）是关键．