
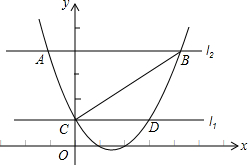
 如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.
如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.分析 (1)根据a、b、c的值,可确定抛物线的解析式,进而可求出C点的坐标;根据t的值,可确定直线L2的解析式,联立抛物线的解析式即可得到A、B的坐标;根据A、B、C三点的坐标,根据勾股定理,可得关于t的方程,根据解方程,可得答案;
(2)根据抛物线的解析式可知:C点坐标为(0,c),那么直线L2的解析式为c+t,联立抛物线的解析式可得到关于x的方程,那么方程的两根即为A、B的横坐标,可由根与系数的关系求出AB的长;根据勾股定理及勾股定理的逆定理,可得答案;
(3)根据菱形的判定有一组邻边相等的两个三角形相似,可得答案.
解答 解:(1)当a=$\frac{1}{2}$,b=-$\frac{3}{2}$,c=1,
y=$\frac{1}{2}$x2-$\frac{3}{2}$x+1,
A、B纵坐标为(t+1),
令y=t+1,解得x=-1或x=4,
故A($\frac{3-\sqrt{9+8t}}{2}$,t+1),B($\frac{3+\sqrt{9+8t}}{2}$,t+1),C(0,1),
△ACB是直角三角形时,
AC2=t2+($\frac{3-\sqrt{9+8{t}^{2}}}{2}$)2,BC2=t2+($\frac{3+\sqrt{9+8t}}{2}$)2,AB2=($\sqrt{9+8t}$)2,
∴AC2+BC2=AB2,
t2+($\frac{3-\sqrt{9+8{t}^{2}}}{2}$)2+t2+($\frac{3+\sqrt{9+8t}}{2}$)2=($\sqrt{9+8t}$)2,
解得t=2,
当△ABC是直角三角形时,t=2;
2)由方程c+$\frac{1}{a}$=ax2+bx+c得ax2+bx-$\frac{1}{a}$=0,
解得x1=$\frac{-b-\sqrt{{b}^{2}+4}}{2a}$,x2=$\frac{-b+\sqrt{b+4}}{2a}$,即A($\frac{-b-\sqrt{{b}^{2}+4}}{2a}$,c+$\frac{1}{a}$),B($\frac{-b+\sqrt{b+4}}{2a}$,c+$\frac{1}{a}$),
设方程的两根为x1、x2,由根与系数的关系得:
x1+x2=-$\frac{b}{a}$,x1x2=-$\frac{1}{{a}^{2}}$;
AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{\sqrt{{b}^{2}+4}}{a}$;
AC2=($\frac{-b-\sqrt{{b}^{2}+4}}{2a}$)2+($\frac{1}{a}$)2,BC2=($\frac{-b+\sqrt{b+4}}{2a}$)2+($\frac{1}{a}$)2,
($\frac{-b-\sqrt{{b}^{2}+4}}{2a}$)2+($\frac{1}{a}$)2+($\frac{-b+\sqrt{b+4}}{2a}$)2+($\frac{1}{a}$)2=($\frac{\sqrt{{b}^{2}+4}}{a}$)2,
当t=$\frac{1}{a}$时,△ABC是直角三角形;
(3)四边形A′CBD是菱形,理由如下:
y=ax2+bx+c,当y=0时,解得x1=0,x2=-$\frac{b}{a}$,即C(0,c)D(-$\frac{b}{a}$,c),CD=-$\frac{b}{a}$.
如图: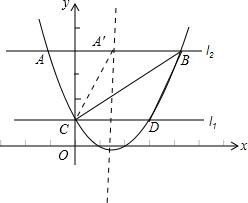 ,
,
因为点A关于y轴的对称点A′恰好在抛物线F的对称轴上,
A($\frac{-b-\sqrt{{b}^{2}+4}}{2a}$,c+$\frac{1}{a}$),A′($\frac{b+\sqrt{{b}^{2}+4}}{2a}$,c+$\frac{1}{a}$),B($\frac{-b+\sqrt{{b}^{2}+4}}{2a}$,c+$\frac{1}{a}$),
∴A′B=-$\frac{b}{a}$;CD=-$\frac{b}{a}$,
∴四边形A′CDB是平行四边形,
$\frac{b+\sqrt{{b}^{2}+4}}{2a}$=-$\frac{b}{2a}$,解得b=-$\frac{2\sqrt{3}}{3}$,
A′C2=($\frac{b+\sqrt{{b}^{2}+4}}{2a}$)2+($\frac{1}{a}$)2,
A′C=-$\frac{b}{a}$=A′B,
四边形A′CDB是菱形.
点评 本题考查了二次函数综合题,函数图象交点坐标的求法、直角三角形的判定和性质、抛物线的对称性、勾股定理以及平行四边形的判定和性质等重要知识点,综合性强,难度较大.


科目:初中数学 来源: 题型:解答题
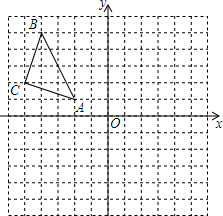 如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
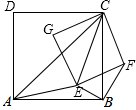 如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.
如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.
如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
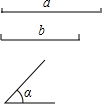 如图,已知线段a、b和∠α,用尺规作一个三角形ABC,使BC=a,AC=b,∠ACB=∠α(要求:不写已知、求作、作法、只画图,保留作图痕迹)
如图,已知线段a、b和∠α,用尺规作一个三角形ABC,使BC=a,AC=b,∠ACB=∠α(要求:不写已知、求作、作法、只画图,保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com