
【题目】某工厂接受了 20 天内生产1200 台GH 型电子产品的总任务。已知每台GH 型产品由 4 个G 型装 置和3 个 H 型装置配套组成。工厂现有80 名工人,每个工人每天能加工6 个G 型装置或3 个 H 型装置。工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G 、H 型装置数量正好组成GH 型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH 型电子产品?
(2)工厂补充 40名新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工 4个G型装置,则补充新工人后每天能配套生产多少产品?补充新工人后20天内能完成总任务吗?
【答案】(1)48;(2)72,能.
【解析】
(1)设安排x名工人生产G型装置,则安排(80﹣x)名工人生产H型装置,根据“生产的装置总数=每人每天生产的数量×人数”结合每台GH型产品由4个G型装置和3个H型装置配套组成,即可得出关于x的一元一次方程,解之可得出x的值,再将其代入![]() 中即可求出结论;
中即可求出结论;
(2)设安排y名工人生产H型装置,则安排(80﹣y)名工人及40名新工人生产G型装置,同(1)可得出关于y的一元一次方程,解之可得出y的值,再将其代入![]() 中即可求出补充新工人后每天能配套生产的套数,进而求出20天生产的总数,与1200比较即可得出结论.
中即可求出补充新工人后每天能配套生产的套数,进而求出20天生产的总数,与1200比较即可得出结论.
(1)设安排x名工人生产G型装置,则安排(80﹣x)名工人生产H型装置,
根据题意得:![]() ,
,
解得:x=32,∴![]() 48.
48.
答:按照这样的生产方式,工厂每天能配套组成48套GH型电子产品.
(2)设安排y名工人生产H型装置,则安排(80﹣y)名工人及40名新工人生产G型装置,
根据题意得:![]() ,
,
解得:y=72,∴![]() y=72.
y=72.
∵72×20=1440>1200,∴补充新工人后20天内能完成总任务.
答:补充新工人后每天能配套生产72套产品,补充新工人后20天内能完成总任务.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
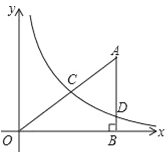
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行,已知老师与学生一共25人参加此次研学旅行,购买门票共花费1700元,门票费用如表格所示,求参加研学旅行的老师和学生各有多少人?设老师有x人,学生有y人,则可列方程组为( )
景点 | 票价 | 开放时间 |
泰山门票 | 旺季:125元/人 淡季:100元/人 | 全天 |
说明:(1)旺季时间(2月~11月),淡季时间(12月-次年1月); (2)老年人(60岁~70岁)、学生、儿童(1.2米~1.4米)享受5折优惠; (3)教师、省部级劳模、英模、道德模范享受8折优惠; (4)现役军人、伤残军人、70岁以上老年人、残疾人,凭本人有效证件免费进山; (5)享受优惠的游客请出示本人有效证件。 | ||
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题一:如图1,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地,若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h), 两车之间距离为y(km).
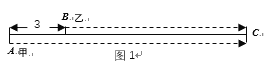
(1)当甲追上乙时,x= .
(2)请用x的代数式表示y.
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 km;时针OE指向圆周上的点的速度为每分钟转动 km.
(2)若从2:00起计时,求几分钟后分针与时针第一次重合?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有三点 A,B,C ,若用 AB 表示 A,B 两点的距离,AC 表示 A ,C 两点的 距离,且 BC 2 AB ,点 A 、点C 对应的数分别是a 、c ,且| a 20 | | c 10 | 0 .
![]()
(1)若点 P,Q 分别从 A,C 两点同时出发向右运动,速度分别为 2 个单位长度/秒、5个单位长度/ 秒,则运动了多少秒时,Q 到 B 的距离与 P 到 B 的距离相等?
(2)若点 P ,Q 仍然以(1)中的速度分别从 A ,C 两点同时出发向右运动,2 秒后,动点 R 从 A点出发向左运动,点 R 的速度为1个单位长度/秒,点 M 为线段 PR 的中点,点 N为线段 RQ的中点,点R运动了x 秒时恰好满足 MN AQ 25,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
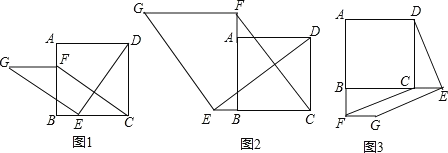
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
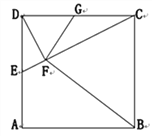
【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com