
【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“![]() (植物园)、
(植物园)、![]() (动物园)、
(动物园)、![]() (湿地公园)、
(湿地公园)、![]() (岳麓山)”四个景点中选择一个,根据调查结果,绘制了两幅不完整的统计图.
(岳麓山)”四个景点中选择一个,根据调查结果,绘制了两幅不完整的统计图.
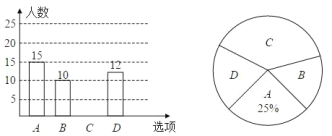
(1)这次问卷调查的人数是_________人;
(2)补全条形统计图;
(3)计算“![]() ”所在扇形的圆心角度数为_________;
”所在扇形的圆心角度数为_________;
(4)若该学校共有3000名学生,则估计该校最想去岳麓山的学生约为_________人.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.
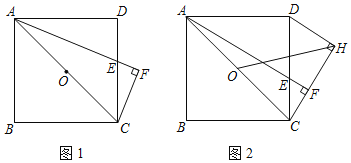
(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;
(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;
(3)当E为DC中点时,AC=2![]() ,直接写出AF的长 .
,直接写出AF的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
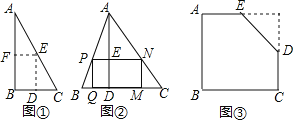
【题目】如图①,是一张直角三角形纸片,∠B=90°,AB=12,BC=8,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大.
(1)请通过计算说明小明的猜想是否正确;
(2)如图②,在△ABC中,BC=10,BC边上的高AD=10,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,求矩形PQMN面积的最大值;
(3)如图③,在五边形ABCDE中,AB=16,BC=20,AE=10,CD=8,∠A=∠B=∠C=90°.小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣16的图象经过点(﹣2,﹣40)和点(6,8).
(1)求这个二次函数图象与x轴的交点坐标;
(2)当y>0时,直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,正方形![]() 的顶点
的顶点![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点(不与端点
边上一动点(不与端点![]() 重合),连接
重合),连接![]() ,作线段
,作线段![]() 的垂直平分线
的垂直平分线![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
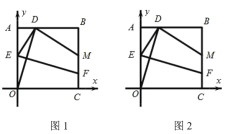
(1)如图1,当点![]() 为线段AB的中点时,求线段
为线段AB的中点时,求线段![]() 的长;
的长;
(2)如图2,若正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,记
,记![]() ,试证明
,试证明![]() 为定值;
为定值;
(3)在(2)的条件下,构造过点C的抛物线![]() 同时满足以下两个条件:
同时满足以下两个条件:
①![]() ;②当
;②当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求二次项系数
,求二次项系数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
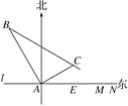
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
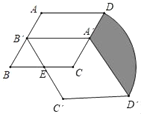
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,把菱形ABCD绕BC的中点E顺时针旋转60°得到菱形A'B'C'D',其中点D的运动路径为![]() ,则图中阴影部分的面积为__.
,则图中阴影部分的面积为__.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
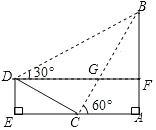
【题目】如图,小明想测量斜坡![]() 旁一棵垂直于地面
旁一棵垂直于地面![]() 的树
的树![]() 的高度,他们先在点
的高度,他们先在点![]() 处测得树顶
处测得树顶![]() 的仰角为
的仰角为![]() ,然后在坡顶
,然后在坡顶![]() 测得树顶
测得树顶![]() 的仰角为
的仰角为![]() ,已知斜坡
,已知斜坡![]() 的长度为
的长度为![]() ,斜坡顶点
,斜坡顶点![]() 到地面的垂直高度
到地面的垂直高度![]() ,则树
,则树![]() 的高度是( )
的高度是( )![]()
A. 20![]() B. 30
B. 30![]() C. 30D. 40
C. 30D. 40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com