
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A、B两点,连接OA、OB,
交于A、B两点,连接OA、OB,![]() 轴于点M,
轴于点M,![]() 轴于点N,有以下结论:①
轴于点N,有以下结论:①![]() ;②
;②![]() ;③
;③![]() 则
则![]() ;④当
;④当![]() 时,
时,![]() .其中结论正确的是___________
.其中结论正确的是___________
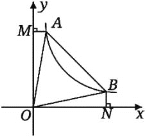
【答案】①②③④
【解析】
①②设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),联立y=-x+b与y=
),联立y=-x+b与y=![]() 得
得![]() ,则
,则![]()
![]() =k,又
=k,又![]()
![]() =k,比较可知
=k,比较可知![]() =
=![]() ,同理可得
,同理可得![]() =
=![]() ,即ON=OM,AM=BN,可证结论;
,即ON=OM,AM=BN,可证结论;
③作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k;
④延长MA,NB交于G点,可证△ABG为等腰直角三角形,当AB=![]() 时,GA=GB=1,则ON-BN=GN-BN=GB=1;
时,GA=GB=1,则ON-BN=GN-BN=GB=1;
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),代入y=
),代入y=![]() 中,得
中,得![]()
![]() =
=![]()
![]() =k,
=k,
联立 ,
,
得![]() ,
,
则![]()
![]() =k,又
=k,又![]()
![]() =k,
=k,
∴![]() =
=![]() ,
,
同理![]()
![]() =k,
=k,
可得![]() =
=![]() ,
,
∴ON=OM,AM=BN,
∵∠AMO=∠BNO=90![]() ,
,
∴△AOM≌△BON,②正确;
∴OA=OB,①正确;
③作OH⊥AB,垂足为H,
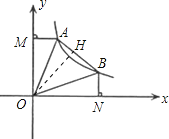
∵OA=OB,∠AOB=45°,且△AOM≌△BON,
∴∠MOA=∠BON=22.5°,∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=![]() ,正确;
,正确;
④延长MA,NB交于G点,
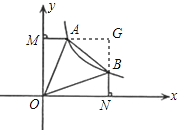
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB![]() 时,GA=GB=1,
时,GA=GB=1,
∴ON-BN=GN-BN=GB=1,正确;
综上,①②③④都正确.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A,B在x轴的负半轴上,反比例函数y=![]() (k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,
(k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,![]() ),直线y=k2x+b(k2≠0)经过点D,点G,则不等式
),直线y=k2x+b(k2≠0)经过点D,点G,则不等式![]() ≤k2x+b的解集为__________.
≤k2x+b的解集为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
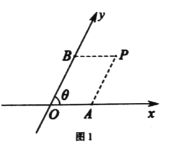
【题目】阅读材料并解答下列问题:如图1,把平面内一条数轴![]() 绕原点
绕原点![]() 逆时针旋转角
逆时针旋转角![]() 得到另一条数轴
得到另一条数轴![]() 轴和
轴和![]() 轴构成一个平面斜坐标系
轴构成一个平面斜坐标系![]()
规定:过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,若点
,若点![]() 在
在![]() 轴对应的实数为
轴对应的实数为![]() ,点
,点![]() 在
在![]() 轴对应的实数为
轴对应的实数为![]() ,则称有序实数对
,则称有序实数对![]() 为点
为点![]() 在平面斜坐标系
在平面斜坐标系![]() 中的斜坐标.如图2,在平面斜坐标系
中的斜坐标.如图2,在平面斜坐标系![]() 中,已知
中,已知![]() ,点
,点![]() 的斜坐标是
的斜坐标是![]() ,点
,点![]() 的斜坐标是
的斜坐标是![]()
(1)连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() (点
(点![]() 与点
与点![]() 对应),求点
对应),求点![]() 的斜坐标;
的斜坐标;
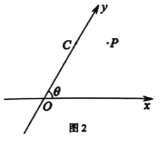
(3)若点![]() 是直线
是直线![]() 上一动点,在斜坐标系
上一动点,在斜坐标系![]() 确定的平面内以点
确定的平面内以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ,当⊙
,当⊙![]() 与
与![]() 轴相切时,求点
轴相切时,求点![]() 的斜坐标,
的斜坐标,
查看答案和解析>>
科目:初中数学 来源: 题型:
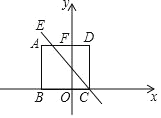
【题目】如图所示, 在平面直角坐标系中, 边长为![]() 的正方形
的正方形![]() 的边
的边![]() 在
在![]() 轴上,
轴上, ![]() 交
交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图像经过点
的图像经过点![]() ,且与线段
,且与线段![]() 始终有交点(含端点),若
始终有交点(含端点),若![]() ,则
,则![]() 的值可能为( )
的值可能为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
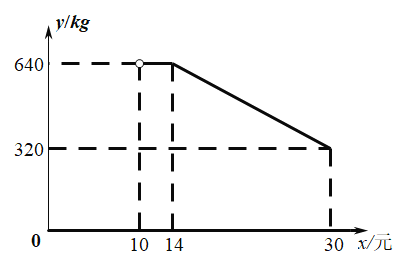
【题目】![]() 年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式。某乡镇贸易公司因此开设了一家网店,销售当地某种农产品。已知该农产品成本为每千克
年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式。某乡镇贸易公司因此开设了一家网店,销售当地某种农产品。已知该农产品成本为每千克![]() 元,调查发现,每天销售量
元,调查发现,每天销售量![]() 与销售单价
与销售单价![]() (元)满足如图所示的函数关系(其中
(元)满足如图所示的函数关系(其中![]() )
)
(1)求![]() 与
与![]() 之间的函数关系式并标出自变最
之间的函数关系式并标出自变最![]() 的取值范围;
的取值范围;
(2)当销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A,B(1,0),与
与x轴交于点A,B(1,0),与![]() 轴交于点C(0,3),对称轴为直线
轴交于点C(0,3),对称轴为直线![]() .
.
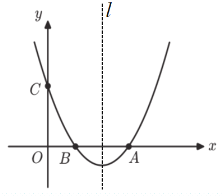
(1)求抛物线的解析式及点A的坐标;
(2)在对称轴![]() 上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
(3)若点P是抛物线上一动点,从点C沿抛物线向点A运动,过点P作PD//![]() 轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作![]() 于点G,交AD于点F.
于点G,交AD于点F.
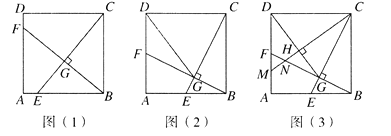
(1)求证:![]() ;
;
(2)如图(2),当点E运动到AB的中点时,连接DG,求证:![]() ;
;
(3)如图(3),在(2)的条件下,过点C作![]() 于点H,分别交AD,BF于点M,N,求证:
于点H,分别交AD,BF于点M,N,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014河南22题)
(1)问题发现
如图①,![]() 和
和![]() 均为等边三角形,点A、D、E在同一条直线上,连接BE;
均为等边三角形,点A、D、E在同一条直线上,连接BE;
填空:
①![]() 的度数为__________;
的度数为__________;
②线段AD、BE之间的数量关系为__________.
(2)拓展探究
如图②,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点A、D、E在同一条直线上,CM为
,点A、D、E在同一条直线上,CM为![]() 中DE边上的高,连接BE.请判断
中DE边上的高,连接BE.请判断![]() 的度数及线段CM、AE、BE之间的数量关系,并说明理由;
的度数及线段CM、AE、BE之间的数量关系,并说明理由;
(3)解决问题
如图③,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点A到BP的距离.
,请直接写出点A到BP的距离.
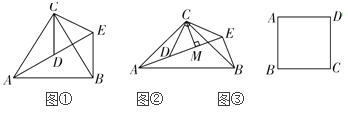
图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A且与x轴平行的直线交抛物线y=![]() (x+1)2于B,C两点,若线段BC的长为6,则点A的坐标为( )
(x+1)2于B,C两点,若线段BC的长为6,则点A的坐标为( )
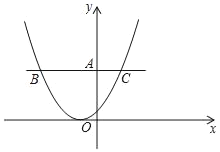
A.(0,1)B.(0,4.5)C.(0,3)D.(0,6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com