Question

18．如图，数轴上的两个点A、B所对应的数分别为-8、7，点M、N对应的数分别是m、m+3．
（1）若AM=BN，请直接写出点M、N所对应的数；

（2）若AN=2BM，求m的值；
（3）设点P为AN的中点，点Q为BM的中点，问当线段MN在数轴上运动时，PQ的值是否发生改变？如果不变，求出PQ的值；如果改变，请说明理由．

Answer 1

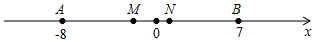
分析 （1）根据AM=BN，MN=3，AB=15，即可得到点M、N所对应的数；
（2）根据A、B所对应的数分别是-8、7，M、N所对应的数分别是m、m+3，可得AN=|（m+3）-（-8）|=|m+11|，BM=|7-m|，分三种情况讨论，即可得到m的值；
（3）设P、Q表示的数为a、b．分两种情况进行讨论，根据点P为AN的中点，点Q为BM的中点，即可得到PQ的值为定值．

解答 解：（1）∵AM=BN=$\frac{7-（-8）-3}{2}$=6，而-8+6=-2，7-6=1，
∴M、N点对应的数分别是-2和1；

（2）∵A、B所对应的数分别是-8、7，M、N所对应的数分别是m、m+3．
∴AN=|（m+3）-（-8）|=|m+11|，BM=|7-m|，
①当m≤-11时，有m+11≤0，7-m＞0．
∴AN=|m+11|=-m-11，BM=|7-m|=7-m，
由AN=2BM得，-m-11=2（7-m），
解得m=25，
∵m≤-11，
∴m=25不合题意，舍去．
②当-11＜m≤7时，有m+11＞0，7-m≥0．
∴AN=|m+11|=m+11，BM=|7-m|=7-m，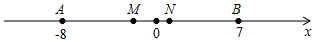
由AN=2BM得，m+11=2（7-m），
解得m=1．
③当m＞7时，有m+11＞0，7-m＜0．
∴AN=|m+11|=m+11，BM=|7-m|=m-7，
由AN=2BM得，m+11=2（m-7），
解得m=25，
综上所述：当m=1或m=25时，AN=2BM．

（3）PQ 的值不发生改变．
设P、Q表示的数为a、b．
∵点P为AN的中点，
∴AP=NP，
①当点N在点A右侧时，点A，N表示的数分别为-8，m+3，
∴AP=a-（-8），NP=（m+3）-a，
∴a-（-8）=（m+3）-a，解得a=$\frac{m-5}{2}$，
同理可得，b=$\frac{m+7}{2}$，
∴PQ=b-a=$\frac{m+7}{2}$-$\frac{m-5}{2}$=6，
②当点N在点A左侧时，同理可得PQ=6，
∴PQ的值不发生改变，恒为6．

点评 本题考查了两点间的距离、数轴以及一元一次方程的运用，表示出两点间的距离是解题的关键，要注意分类讨论．