
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2��![]() x+c��ֱ��y��
x+c��ֱ��y��![]() x+
x+![]() ����A��B���㣬��֪��B�ĺ�������4��ֱ��y��
����A��B���㣬��֪��B�ĺ�������4��ֱ��y��![]() x+
x+![]() ��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮
��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮

��1���������ߵĽ���ʽ��
��2������P��ֱ��y��![]() x+
x+![]() �·������PAC����������
�·������PAC����������
��3����M�������߶Գ����ϵ�һ�㣬�Ե�A��B��P��MΪ������ı����ܷ��Ϊƽ���ı��Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��y��![]() x2��
x2��![]() x��
x��![]() ����2��
����2��![]() ����3����P����������6��
����3����P����������6��![]() ����4��
����4��![]() ����2����
����2����![]() ����
����
��������
��1����ֱ��y��![]() x+
x+![]() ��x��y��Ľ���ֱ�ΪA��C���ó���A�����꣬��x=4����ֱ��y��
��x��y��Ľ���ֱ�ΪA��C���ó���A�����꣬��x=4����ֱ��y��![]() x+
x+![]() �����yֵ�����ɵó���B���꣬�ɵ�A��B������������ô���ϵ����������������ߵĽ���ʽ��
�����yֵ�����ɵó���B���꣬�ɵ�A��B������������ô���ϵ����������������ߵĽ���ʽ��
��2������P��y���ƽ���߽�AB�ڵ�H�����P�����꣬��ʾ��H�����꣬���÷ָ�ͼ�η�������ҳ�S��PAC����x�Ķ��κ�����ϵʽ�����ݶ��κ��������ʼ��ɽ����ֵ���⣻
��3�������ܣ����߶�ABΪ�Խ��ߺͱ�������������ǣ�����ƽ�Ƶ����ʺ��е㹫ʽ���P��ĺ����꣬������������߽���ʽ�м��ɵó���P�����꣮
�⣺��1��y��![]() x+
x+![]() ����y��0����x����1���ʵ�A����1��0����
����y��0����x����1���ʵ�A����1��0����
��B�������4�����B��4��2����
����A��B��������������߱���ʽ�ã� ����ã�
����ã� ��
��
�������ߵı���ʽΪ��y��![]() x2��
x2��![]() x��
x��![]() ��
��
��2������P��y���ƽ���߽�AB�ڵ�H��

���P��x��![]() x2��
x2��![]() x��
x��![]() �������H��x��
�������H��x��![]() x+
x+![]() ��
��
���PAC���S��S��PHA��S��PHC��![]() PH��xC��xA��
PH��xC��xA��
��![]() ����
����![]() x+
x+![]() ��
��![]() x2+
x2+![]() x+
x+![]() ��
��
����![]() x2+
x2+![]() x+
x+![]() ��
��
��![]() ��0����S�����ֵ��
��0����S�����ֵ��
��x��![]() ʱ��S�����ֵΪ��
ʱ��S�����ֵΪ��![]() ��
��
��3���ܣ����ɣ�
���P������Ϊ����m��n������M��1��s��������A��B������ֱ�Ϊ������1��0������4��2����
�ٵ�AB�DZ�ʱ��
��A����ƽ��5����λ������ƽ��2����λ�õ�B��
ͬ������P��M������ƽ��5����λ������ƽ��2����λ�õ�M��P����
��1+5��m��1��5��m��
��ã�m��6��4����n��![]() ��
��
�ʵ�P��6��![]() ����4��
����4��![]() ����
����
�ڵ�AB�ǶԽ���ʱ��
���е㹫ʽ�ã�m+1��4��1��
��ã�m��2���ʵ�P��2����![]() ����
����
���ϣ���P������Ϊ����6��![]() ����4��
����4��![]() ����2����
����2����![]() ����
����


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO��CO��BO��DO���ҡ�ABC+��ADC��180����
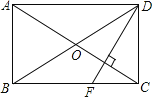
��1����֤���ı���ABCD�Ǿ��Σ�
��2������ADF����FDC��3��2��DF��AC�����BDF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A1,A2,��,An����ֱ��![]() �ϣ���B1,B2,��,Bn����˫����
�ϣ���B1,B2,��,Bn����˫����![]() �ϣ��������㣺A1B1��x�ᣬB1A2��y�ᣬA2B2��x�ᣬB2A3��y�ᣬ��,AnBn��x�ᣬBnAn+1��y�ᣬ�����ǵ�An�ĺ�����Ϊ
�ϣ��������㣺A1B1��x�ᣬB1A2��y�ᣬA2B2��x�ᣬB2A3��y�ᣬ��,AnBn��x�ᣬBnAn+1��y�ᣬ�����ǵ�An�ĺ�����Ϊ![]() (nΪ������)����
(n������)����![]() ����
����![]() __��
__��![]() __��
__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB��BC����ABΪֱ���İ�Բ�ֱ�AC��BC�ڵ�D��E���㣬BF����O�����ڵ�B����AC���ӳ����ڵ�F��
��1����֤��D��AC���е㣻
��2����AB��12��sin��CAE��![]() ����CF��ֵ��
����CF��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ˮƽ��������ߣ�����Խ��Խϲ�����ڣ����յ���ʽ���ս�Ũ�ң�ijУ��������Ů���ů���ر��ж�����������������˲���ͬѧ��ů���ж����������ΪA��B��C��D�������ͣ��ֱ��Ӧ�ͷ������ʻ����ͺ�����ͻ�����ָ��ݵ�������ݻ��Ƴ����µ�����ͳ��ͼ������ͳ��ͼ��

��������ϲ�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1����У������˶�����ͬѧ��ů���ж���
��2����ȫ����ͳ��ͼ������ͳ��ͼ��
��3������У����2400��ͬѧ������Ƹ�У�������ʻ��ж���ͬѧԼ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����![]() ��ԭ��
��ԭ��![]() ����ʱ�뷽����ת
����ʱ�뷽����ת![]() �õ���
�õ���![]() �����
�����![]() �������� ��
�������� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�۲����
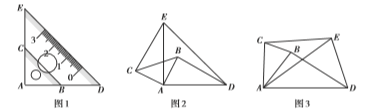
��ͼ1���й���ֱ�Ƕ���![]() ��������ȫ�ȵĵ���ֱ�����dzߵ�����һ�𣬵�
��������ȫ�ȵĵ���ֱ�����dzߵ�����һ�𣬵�![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��.
��.
��1����ͼ1�У��㷢���߶�![]() ��
��![]() ��������ϵ��___________��ֱ��
��������ϵ��___________��ֱ��![]() ��
��![]() ��λ�ù�ϵ��________.
��λ�ù�ϵ��________.
��������
��2����ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ����ǵõ�ͼ2����ʱ��1���е����������Ƿ�����������жϲ�˵�����ɣ�
��ʱ����תһ����ǵõ�ͼ2����ʱ��1���е����������Ƿ�����������жϲ�˵�����ɣ�
�ع�̽��
��3����ͼ3����ֻ�����й���ֱ�Ƕ���![]() ��������ȫ�ȵĵ���ֱ�����dz�����Ϊ���й�������Ϊ
��������ȫ�ȵĵ���ֱ�����dz�����Ϊ���й�������Ϊ![]() ����ǣ���������ȫ�ȵ�������������
����ǣ���������ȫ�ȵ�������������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת����һ����ǣ���ʱ��1���е�����������Ȼ�����������жϣ�����˵������.
��ʱ����ת����һ����ǣ���ʱ��1���е�����������Ȼ�����������жϣ�����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ�����Ҫ�������⣺
���⣺����ƽ���ڣ���֪�ֱ���2���㣬3���㣬4���㣬5���㣬����![]() ���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
̽����Ϊ�˽��������⣬ϣ��С���ͬѧ�ǣ���������±������̽������Ϊ�˷����о����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���� | 2 | 3 | 4 | 5 | �� |
|
ʾ��ͼ |
|
|
|
| �� |
|
ֱ������ | 1 |
|
|
| �� |
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ������![]() ����ʱ��ֱ������Ϊ______��
����ʱ��ֱ������Ϊ______��
��2����ijͬѧ���ձ����еķ�����������28��ֱ�ߣ����ƽ�����ж��ٸ���֪�㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�鳤���ε����أ���Ϊ120m�������̰����ֳɼס��ҡ��������֣����Ҿ�Ϊ�����Σ��ּƻ���סլ�����ҽ��̳������ؿ��ٳ����Ϊ3200m2�Ĺ���������鳤���ε����س�Ϊxm����ô���������г��ķ�����_____��������д��ax2+bx+c=0��a��0������ʽ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com