
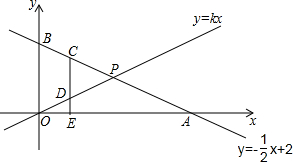
 一次函数y=-$\frac{1}{2}$x+2的图象在平面直角坐标系中交x轴、y轴分别于A、B两点,交直线y=kx于P.
一次函数y=-$\frac{1}{2}$x+2的图象在平面直角坐标系中交x轴、y轴分别于A、B两点,交直线y=kx于P.分析 (1)根据题意知,一次函数y=ax+b的图象过点B(0,2)和点A(4,0),把A、B代入求值即可;
(2)设P(x,y),根据PO=PA,列出方程,并与y=kx组成方程组,解方程组;
(3)设点C(x,-$\frac{1}{2}$x+2),再根据等量关系CD=2ED列方程求解.
解答 解:(1)当x=0时,y=-$\frac{1}{2}$x+2=2,
∴B(0,2)
当y=0时,y=-$\frac{1}{2}$x+2=0,
∴x=4,
∴A(4,0);
(2)设P(x,y),因为点P在直线y=-$\frac{1}{2}$x+2,
且OP=AP,
∴x=2,
把x=2代入y=-$\frac{1}{2}$x+2,y=1,所以点P的坐标是(2,1),
因为点P在直线y=kx上,所以k=$\frac{1}{2}$;
(3)设点C(x,-$\frac{1}{2}$x+2),则D(x,$\frac{1}{2}$x),E(x,0),
因为CD=2DE,所以-$\frac{1}{2}$x+2-$\frac{1}{2}$x=2×$\frac{1}{2}$x,
解得:x=1,则-$\frac{1}{2}$x+2=$\frac{3}{2}$,
所以点C的坐标为(1,$\frac{3}{2}$).
点评 本题要求利用图象求解各问题,要认真体会点的坐标,一次函数与一元一次方程组之间的内在联系.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | $\sqrt{2}$ | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直相交,平行 | D. | 平行,垂直相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.3}$和$\sqrt{0.03}$ | B. | $\sqrt{\frac{2}{3}}$和$\sqrt{54}$ | C. | $\sqrt{12}$和$\sqrt{0.75}$ | D. | $\sqrt{\frac{4}{5}}$和$\sqrt{{2}^{2}+{4}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
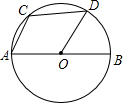 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com