
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC,外角∠CAM的平分线,CE⊥AN,垂足为点E.
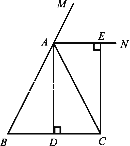
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
【答案】(1)证明见解析;
(2)当AD= ![]() 时,四边形ADCE是正方形,证明见解析.
时,四边形ADCE是正方形,证明见解析.
【解析】试题分析:(1)求出∠BAD=∠DAC,∠MAE=∠CAE,求出∠DAE的度数,求出∠AEC=∠ADC=∠EAD=90°,根据矩形的判定判断即可;
(2)求出AD=DC,得出∠ACD=∠DAC=45°,求出∠BAC=90°,即可求出答案.
试题解析:(1)证明:∵在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE.
∴∠DAE=∠DAC+∠CAE=![]() ∠MAC+
∠MAC+![]() ∠CAB=
∠CAB=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)证明:∵四边形ADCE是正方形,
∴DC=AD,
∵在△ABC中,AB=AC,AD⊥BC,
∴△ADC为等腰直角三角形,
∴∠DAC=∠ACD=45°,
∴∠BAC=90°,
∴△ABC为等腰直角三角形,
即△ABC的形状是等腰直角三角形.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() 的解满足x<0,y>0.
的解满足x<0,y>0.
(1)x=________, y=________(用含a的代数式表示);
(2)求a的取值范围;
(3)若2x8y=2m,用含有a的代数式表示m,并求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( ).
① 相等的角是对顶角;② 同旁内角互补;③ 在同一平面内,若a//b,b//c,则a//c;④ 末位是零的整数能被5整除.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
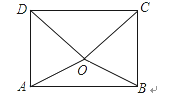
【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院观众席的座位设置为扇形,且按下列方式排布:

(1)按照上表所表示的变化规律,当排数![]() 每增加1时,座位数
每增加1时,座位数![]() 如何变化?
如何变化?
(2)写出座位数![]() 与排数
与排数![]() 之间的关系式.
之间的关系式.
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案: 方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com