
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x2+bx+c��x�ύ��B��C���㣬��y�ύ�ڵ�A��ֱ��y����
x2+bx+c��x�ύ��B��C���㣬��y�ύ�ڵ�A��ֱ��y����![]() x+2����A��C���㣬�����ߵĶԳ�����x�ύ�ڵ�D��ֱ��MN��Գ��ύ�ڵ�G���������߽���M��N���㣨��N�ڶԳ����Ҳࣩ����MN��x�ᣬMN��7��
x+2����A��C���㣬�����ߵĶԳ�����x�ύ�ڵ�D��ֱ��MN��Գ��ύ�ڵ�G���������߽���M��N���㣨��N�ڶԳ����Ҳࣩ����MN��x�ᣬMN��7��
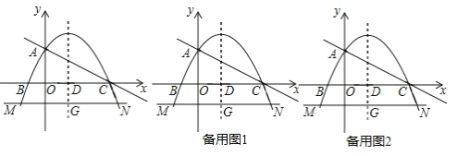
��1����������ߵĽ���ʽ��
��2�����N�����꣮
��3������A��ֱ���������߽��ڵ�F����tan��FAC��![]() ʱ�����F�����꣮
ʱ�����F�����꣮
��4������D��ֱ��AC�Ĵ��ߣ���AC�ڵ�H����y���ڵ�K������CN����AHK������AC��ÿ��1����λ���ȵ��ٶ��ƶ����ƶ������С�AHK���ı���DGNC�����ص������ص����ΪS���ƶ�ʱ��Ϊt��0��t��![]() ������ֱ��д��S��t�ĺ�����ϵʽ��
������ֱ��д��S��t�ĺ�����ϵʽ��
���𰸡���1��y����![]() x2+
x2+![]() x+2����2����N��������5��-3������3����F����������3��2����
x+2����2����N��������5��-3������3����F����������3��2����![]() ����
����![]() ������4��
������4�� ��
��
��������
��1����A��C������ֱ�Ϊ��0��2������4��0��������A��C������������߱���ʽ������⣻
��2�������ߵĶԳ���Ϊ��x��![]() ����N�ĺ�����Ϊ��
����N�ĺ�����Ϊ��![]() ��������⣻
��������⣻
��3���ֵ�F��ֱ��AC�·�����F��ֱ��AC���Ϸ�����������ֱ���⼴�ɣ�
��4����0��t��![]() ����
����![]() ��t��
��t��![]() ��
��![]() ��t��
��t��![]() ����������ֱ���⼴�ɣ�
����������ֱ���⼴�ɣ�
�⣺��1��ֱ��y����![]() x+2����A��C���㣬���A��C������ֱ�Ϊ��0��2������4��0����
x+2����A��C���㣬���A��C������ֱ�Ϊ��0��2������4��0����
��c��2�������߱���ʽΪ��y����![]() x2+bx+2��
x2+bx+2��
����C���������ʽ����ã�b��![]() ��
��
�������ߵı���ʽΪ��y����![]() x2+
x2+![]() x+2���٣�
x+2���٣�
��2�������ߵĶԳ���Ϊ��x��![]() ��
��
��N�ĺ�����Ϊ�� ![]() ��
��
�ʵ�N������Ϊ��5��-3����
��3����tan��ACO��![]() ��tan��FAC��
��tan��FAC��![]() ��
��
����ACO����FAC��
�ٵ���F��ֱ��AC�·�ʱ��
��ֱ��AF��x���ڵ�R��

�ߡ�ACO����FAC����AR��CR��
���R��r��0������r2+4����r��4��2����ã�r��![]() ��
��
����R����������![]() ��0����
��0����
����R��A���������һ�κ�������ʽ��y��mx+n�ã� ��
��
��ã� ��
��
��ֱ��AR�ı���ʽΪ��y����![]() x+2���ڣ�
x+2���ڣ�
�����٢ڲ���ã�x��![]() ���ʵ�F��
���ʵ�F��![]() ����
����![]() ����
����
�ڵ���F��ֱ��AC���Ϸ�ʱ��
�ߡ�ACO����F��AC����AF���x�ᣬ
���F�䣨3��2����
���ϣ���F������Ϊ����3��2����![]() ����
����![]() ����
����
��4����ͼ2�����ACO��������tan����![]() ����sin����
����sin����![]() ��cos����
��cos����![]() ��
��
�ٵ�0��t��![]() ʱ�����ͼ����
ʱ�����ͼ����
���AHK�ƶ�����A��H��K���λ��ʱ��ֱ��H��K��ֱ�x���ڵ�T���������߶Գ����ڵ�S��
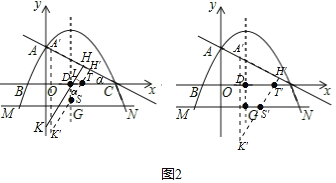
���DST����ACO����������T��TL��KH��
��LT��HH�䣽t����LTD����ACO������
��DT��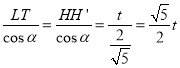 ��DS��
��DS��![]() ��
��
S��S��DST��![]() DT��DS��
DT��DS��![]() ��
��
�ڵ�![]() ��t��
��t��![]() ʱ���Ҳ�ͼ����
ʱ���Ҳ�ͼ����
ͬ���ɵã�
S��![]() ��
��![]() DG����GS��+DT�䣩��
DG����GS��+DT�䣩��![]() 3+��
3+��![]() +
+![]() ��
��![]() ����
����![]() ��
��
�۵�![]() ��t��
��t��![]() ʱ��ͬ���ɵ�S=
ʱ��ͬ���ɵ�S=![]() ��
��
���ϣ�S�� ��
��


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���C=90������A=60����AC=2cm����Ϊ1cm���߶�MN����ABC�ı�AB����AB������1cm/s���ٶ����B�˶����˶�ǰ��M���A�غϣ�����M��N�ֱ���AB�Ĵ��߽�ֱ�DZ���P��Q���㣬�߶�MN�˶���ʱ��Ϊts��

��1������0��t��1��ʱ��PM=____________ ��QN=___________(��t�Ĵ���ʽ��ʾ)��
��2���߶�MN�˶������У��ı���MNQP�п��ܳ�Ϊ���������п��ܣ������ʱt��ֵ���������ܣ�˵�����ɣ�
��3��tΪ��ֵʱ����C��P��QΪ���������������ABC���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y����x+4�ֱ���x�ᡢy�ύ�ڵ�A��B��˫����![]() ��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��
��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС��Ϊ������ͼ������ʾ��һ�ιų�ǽ�ĸ߶ȣ������ƽ�澵������ʾ��ͼ��ͼ����ʾ����P����һˮƽ��ƽ�澵�����ߴӵ�A��������ƽ�澵�����պ��䵽�ų�ǽCD�Ķ���C����

��1����֪AB��BD��CD��BD���Ҳ��AB=1.2m��BP=1.8m.PD=12m����ó�ǽ�ĸ߶ȣ�ƽ�澵��ԭ�Ⱥ��Բ��ƣ���
��2���������һ��������ιų�ǽ�߶ȵķ�����
Ҫ�����ʾ��ͼ����Ҫ��д����������д��������������Ҫ�ļ�����̣��۸����ķ��������õ�ͼ�ڵķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=4��E��AC���е㣬D��ֱ��BC��һ���㣬�߶�ED�Ƶ�E��ʱ����ת90�����õ��߶�EF������D�˶�ʱ����AF����СֵΪ�� ��
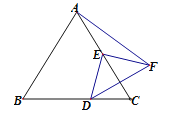
A.2B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C��90������б��ABΪ��������������ABDE���������ζԽ��߽��ڵ�O������OC����֪AC��3��OC��6![]() ������һֱ�DZ�BC�ij�Ϊ_____��
������һֱ�DZ�BC�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�DΪб��AB���е㣬��B=60�㣬BC=2cm������E�ӵ�A������AB���B�˶�������F�ӵ�D������������D��C��B�˶���������ٶȾ�Ϊ1cm/s�������յ��ֹͣ�˶�����AE�ij�Ϊx����AEF�����Ϊy����y��x��ͼ�����Ϊ��������

A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P����ABC�ڣ��������APB=��APC(����ͼ)����APB+��BAC=180����
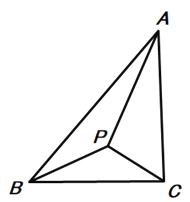
��1����֤����PAB�ס�PCA��
��2������ͼ�������APB=120������ABC=90����![]() ��ֵ��
��ֵ��
��3����ͼ������BAC=45������ABCΪ����������ʱ����tan��PBC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ȤС��������ѧϰ�����ľ��飬�Ժ���y��x+![]() ��ͼ������ʽ�����̽����̽���������£��벹������
��ͼ������ʽ�����̽����̽���������£��벹������
��1������y��x+![]() ���Ա���ȡֵ��Χ���� ����
���Ա���ȡֵ��Χ���� ����
��2���±���x��y�ļ����Ӧֵ

�����m��ֵΪ�� ����
��3�����ݱ������ݣ�����ͼ��ʾƽ��ֱ������xOy����㣬������������һ���֣��뻭���ú�����ͼ�����һ���֣�
��4���۲�����ͼ��д���ú�����һ�����ʣ��� ����
��5����һ��̽�����֣�����y��x+![]() ͼ����ֱ��y����2ֻ��һ���㣬���Է���x+
ͼ����ֱ��y����2ֻ��һ���㣬���Է���x+![]() ����2ֻ��1��ʵ������������x+
����2ֻ��1��ʵ������������x+![]() ��k��x��0������������ȵ�ʵ��������k��ȡֵ��Χ���� ����
��k��x��0������������ȵ�ʵ��������k��ȡֵ��Χ���� ����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com