
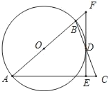
【题目】如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.
【答案】(1)证明参见解析;(2)3.
【解析】试题分析:(1)连接OD,AD,由切线的性质可得OD⊥EF,再利用圆周角定理证明AD⊥BC,根据等腰三角形的性质可证明OD∥AC,由平行线的性质即可得到EF⊥AC;(2)设⊙O的半径为x,由OD∥AC,可得:△ODF∽△AEF,根据相似三角形的性质:对应边的比值相等即可得到关于x的比例式,求出x的值即可.
试题解析:(1)如图:连接OD,AD,
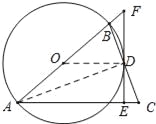
∵EF是⊙O的切线,∴OD⊥EF.又∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC.又∵AB=AC,∴BD=DC.∴OD∥AC.∴AC⊥EF;(2)先设⊙O的半径为x.∵OD∥AE,∴△ODF∽△AEF.∴![]() ,∵BF=2,CE=1.2,∴AE=AC-CE=AB-CE=2x-1.2,OF=OB+BF=x+2,AF=AB+BF=2x+2,所以
,∵BF=2,CE=1.2,∴AE=AC-CE=AB-CE=2x-1.2,OF=OB+BF=x+2,AF=AB+BF=2x+2,所以![]() .解得:x=3.∴⊙O的半径为3.
.解得:x=3.∴⊙O的半径为3.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
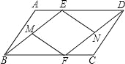
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名外地民工10天的收支情况如下(收入为正):
30元,-17元,21元,-5元,-3元,18元,-21元,45元,-10元,28元.这10天内这名外地民工净收入多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】10袋小麦以每袋150千克为标准,超过150千克的部分记为正数,不足150千克的部分记为负数,记录情况如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
差值/kg | -6 | -3 | -1 | +7 | +3 | +4 | -3 | -2 | -2 | +1 |
(1)与标准重量相比较,10袋小麦总计超过或不足多少千克?
(2)每袋小麦的平均重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着交通网络的不断完善,我市近郊游持续升温.据统计,在今年“五一”期间,某风景区接待游览的人数约为20.3万人,这一数据用科学记数法表示为( )
A.20.3×104人
B.2.03×105人
C.2.03×104人
D.2.03×103人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com