练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知C为直线AB上的点，AB=5，BC=6，则AC=
    11或1
    11或1
    ．
    分析：分类讨论：当C点在射线AB上，则AC=AB+BC；当C点在射线BA上，则AC=CB-AB，然后把AB=5，BC=6分别代入计算即可．
    解答：解：当C点在射线AB上，如图1，
    则AC=AB+BC，
    而AB=5，BC=6，
    ∴AC=5+6=11；
    当C点在射线BA上，如图2，
    则AC=CB-AB，
    ∴AC=6-5=1，
    ∴AC的长为11或1．
    故答案为11或1．
    点评：本题考查了两点间的距离：两点之间的连线段的长叫这两点之间的距离．也考查了分类讨论思想的运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知O为直线AB上的一点，∠COE是直角，OF平分∠AOE．
    （1）如图1，若∠COF=34°，则∠BOE=
     
    ；若∠COF=n°，则∠BOE=
     
    ；∠BOE与∠COF的数量关系为
     
    ．
    （2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF的数量关系是否仍然成立？如成立请写出关系式；如不成立请说明理由．
    （3）在图3中，若∠COF=65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    33、已知O为直线AB上的一点，∠COE是直角，OF 平分∠AOE．
    （1）如图1，若∠COF=34°，则∠BOE=
    68°
    ；若∠COF=m°，则∠BOE=
    2m°
    ；∠BOE与∠COF的数量关系为
    ∠BOE=2∠COF
    ．
    （2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF的数量关系是否仍然成立？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013年四川成都成华区七年级上学期半期考试数学试卷（带解析） 题型：解答题

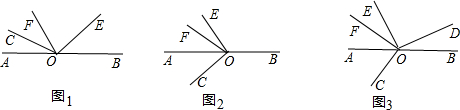
    已知O为直线AB上的一点，∠COE是直角， OF 平分∠AOE．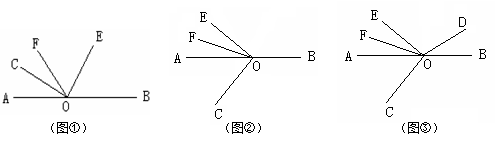

    （1）如图①，若∠COF＝34°，则∠BOE＝      °；若∠COF＝m°，则∠BOE＝      °；由上面的解答可知：∠BOE与∠COF之间的数量关系应该为                ．
    （2）如图②，（1）中∠BOE与∠COF之间的数量关系是否仍然成立？若成立，请给予证明；若不成立，请说明理由．
    （3）如图③，在（2）的情况下，若∠COF＝65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2015届四川成都成华区七年级上学期半期考试数学试卷（解析版） 题型：解答题

    已知O为直线AB上的一点，∠COE是直角， OF 平分∠AOE．

    （1）如图①，若∠COF＝34°，则∠BOE＝      °；若∠COF＝m°，则∠BOE＝      °；由上面的解答可知：∠BOE与∠COF之间的数量关系应该为                ．

    （2）如图②，（1）中∠BOE与∠COF之间的数量关系是否仍然成立？若成立，请给予证明；若不成立，请说明理由．

    （3）如图③，在（2）的情况下，若∠COF＝65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案