[题目]如图.四边形ABCD中.AD∥BC.∠ABD＝30°.AB＝AD.DC⊥BC于点C.若BD＝2.求CD的长．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，四边形ABCD中，AD∥BC，∠ABD＝30°，AB＝AD，DC⊥BC于点C，若BD＝2，求CD的长．

【答案】证明：∵ AD="AB"

∴∠ADB＝∠ABD=300

又∵ AD∥BC

∴∠DBC＝∠ABD=300

∵ DC⊥BC ∴△DBC为直角三角形

在Rt△DBC中，∵∠DBC=300

∴CD=BD=

【解析】

由已知可求得∠ABD＝∠DBC＝30°，已知DC⊥BC，则根据直角三角形中30度所对的边是斜边的一半求解即可．

∵AD∥BC，∴∠ADB＝∠DBC．

又∵AB＝AD，∴∠ADB＝∠ABD，∴∠DBC＝∠ABD＝30°．

∵DC⊥BC于点C，∴∠C＝90°．

在Rt△BDC中，∵∠DBC＝30°，BD＝2，∴CD，∴CD＝1．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图, 已知A（-4，-1），B（-5，-4），C（-1，-3），△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。

（1）请在图中作出△A′B′C′；（2）写出点A′、B′、C′的坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】先化简，再求值：|﹣2|﹣（ ﹣π）0+tan45°+（）﹣1 ．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】小敏和小强到某厂参加社会实践活动，该厂用白板纸做包装盒，每张白板纸可裁成3个盒身或5个盒盖，且一个盒身和两个盒盖恰好能做成一个包装盒．设裁成盒身的白板纸有x张，请回答下列问题：

(1)若有11张白板纸．

①请完成下表：

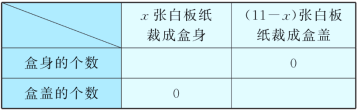
②问：最多可做多少个包装盒．

(2)若仓库中已有4个盒身，3个盒盖和23张白板纸，现把白板纸分成两部分，一部分裁成盒身，一部分裁成盒盖．当盒身与盒盖全部配套用完时，可做多少个包装盒？

(3)若有n张白板纸(70≤n≤80)，先把一张白板纸裁出2个盒身和1个盒盖(余下一点边角料不要)，剩下白板纸分成两部分，一部分裁成盒身，一部分裁成盒盖．当盒身与盒盖全部配套用完时，n的值可以是______．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且AD=CD，求∠ACB的度数．
（3）如图2，△ABC中，AC=2，BC= ，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．