Question

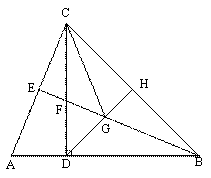
如图，在△ABC中，AB=BC，CD⊥AB于点D， CD＝BD，BE平分∠ABC，点H是BC边的中点，连接DH，交BE于点G，连接CG．

(1)求证：△ADC≌△FDB；(2)求证：CE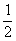＝BF；

(3)判断△ECG的形状，并证明你的结论；

(4)猜想BG与CE的数量关系，并证明你的结论．

 

Answer 1

(1) （本小题4分）∵AB=BC，BE平分∠ABC，∴BE⊥AC，CE＝AE，∵CD⊥AB，得∠ACD＝∠DBF，又CD＝BD，所以有△ADC≌△FDB（4分）；

(2) （本小题4分）∵△ADC≌△FDB，∴AC＝BF，又∵CE＝AE，得CE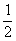＝BF（4分）；

(3) （本小题3分）△ECG为等腰直角三角形（1分）.由点H是BC边的中点，得GH垂直平分BC，从而有GC＝GB，则∠DBF＝∠GBC＝∠GCB＝∠ECF，得∠ECO＝45°，又BE⊥AC，∴△ECG为等腰直角三角形（3分）；

(4) （本小题3分）GB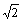＝CE（1分）.∵△ECG为等腰直角三角形，∴GC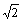＝CE，∵GC＝GB，∴GB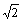＝CE（3分）