
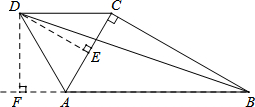
 ,以AC为边在△ABC的外部作等边△ACD,连接BD.
,以AC为边在△ABC的外部作等边△ACD,连接BD.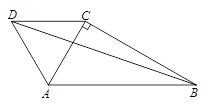
 ;(2)
;(2) .
. AC•BC=
AC•BC= ,再过点D作DE⊥AC于E,解直角△ADE,得出DE=
,再过点D作DE⊥AC于E,解直角△ADE,得出DE= ,则△ACD的面积=
,则△ACD的面积= AC•DE=
AC•DE= ,则根据四边形ABCD的面积=△ABC的面积+△ACD的面积求解.
,则根据四边形ABCD的面积=△ABC的面积+△ACD的面积求解. ,则BF=AF+AB=5,然后在直角△BDF中运用勾股定理即可求出BD的长度.
,则BF=AF+AB=5,然后在直角△BDF中运用勾股定理即可求出BD的长度.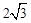 ,
, AC•BC=
AC•BC= ×2×
×2×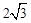 =
=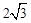 .
.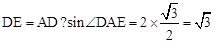 .
. AC•DE=
AC•DE= ×2×
×2× =
= .
.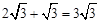 .
. .
. .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
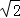 ≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.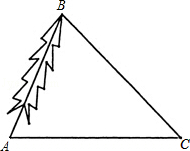
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
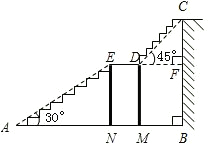 每平方米120元的地毯,求用地毯铺满整个楼梯共需要花费多少元钱?(结果精确到1元)
每平方米120元的地毯,求用地毯铺满整个楼梯共需要花费多少元钱?(结果精确到1元)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
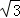 ≈1.73,结果保留整数)
≈1.73,结果保留整数)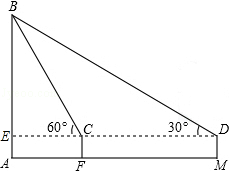
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
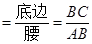 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:如图②,已知sinA
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:如图②,已知sinA ,其中∠A为锐角,试求sadA的值。
,其中∠A为锐角,试求sadA的值。
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 B.
B.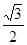 C.
C.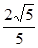 D.
D.
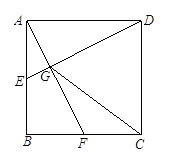
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com