
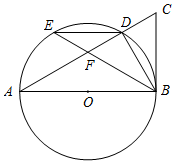
 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.分析 (1)由AB为⊙O的直径,得到∠ADB=90°,根据圆周角定理得到∠A=∠E,得到AB⊥BC,于是得到结论;
(2)根据圆周角定理得到∠A=∠E=∠CBD=30°,得到∠DBA=60°,根据三角函数的定义即可得到结论.
解答 (1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠A+∠DBA=90°,
∵$\widehat{BD}$=$\widehat{BD}$,
∴∠A=∠E,
∵∠CBD=∠E,
∴∠CBD=∠A,
∴∠CBD+∠DBA=90°,
∴AB⊥BC,
∴BC是⊙O的切线,
(2)解:∵∠BED=30°,
∴∠A=∠E=∠CBD=30°,
∴∠DBA=60°,
∵点E为弧AD的中点,
∴∠EBD=∠EBA=30°,
∵⊙O半径为2,
∴AB=4,BD=2,AD=2$\sqrt{3}$,
在Rt△BDF中,∠DBF=90°,
tan∠DBF=$\frac{DF}{BD}$=$\frac{\sqrt{3}}{3}$,
∴DF=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了切线的判定和性质,三角函数的定义,圆周角定理,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 15 | 20 | 25 |
| 千克(千克) | 30 | 40 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
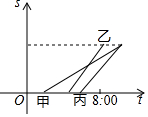 甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )
甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 甲车和乙车 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
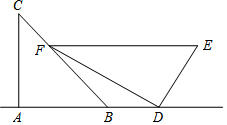 小华是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=2$\sqrt{3}$.
小华是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com