
【题目】如图,已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
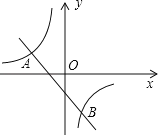
(1)求m、n的值;
(2)求一次函数的关系式;
(3)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
【答案】(1)m=﹣8,n=2;(2)y=﹣x﹣2;(3)x>2或﹣4<x<0.
【解析】
试题分析:(1)把A(﹣3,1)代入y=![]() 求出m=﹣3,得出反比例函数的解析式,把B(2,n)代入反比例函数的解析式求出n,得出B的坐标;
求出m=﹣3,得出反比例函数的解析式,把B(2,n)代入反比例函数的解析式求出n,得出B的坐标;
(2)把A、B的坐标代入一次函数的解析式得出方程组,求出方程组的解即可;
(3)根据图形和A、B的横坐标即可得出答案.
解:(1)把A(﹣4,2)代入y=![]() 得:m=﹣8,
得:m=﹣8,
即反比例函数的解析式为y=﹣![]() ,
,
把B(n,﹣4)代入得:n=2,
即B(2,﹣4),
即m=﹣8,n=2;
(2)把A、B的坐标代入一次函数的解析式得:![]()
解得:k=﹣1,b=﹣2,
即一次函数的解析式是y=﹣x﹣2;
(3)一次函数的值小于反比例函数的值的x的取值范围是x>2或﹣4<x<0.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③(x﹣2)(x+5)=x2﹣1;④3x2﹣![]() =0.
=0.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数按要求填入相应的大括号里:
-10,4.5,- ![]() , 0,-(-3),2.10010001…,-π,
, 0,-(-3),2.10010001…,-π,
整数集合:{ },分数集合:{ },
正有理数集合:{ },无理数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+m.
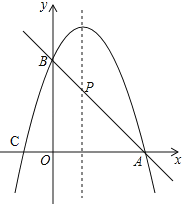
(1)如果抛物线过点A(3,0),与y轴交于点B,求抛物线的解析式及点B、C的坐标;
(2)如图,直线AB与这条抛物线的对称轴交于点P,求直线AB的表达式和点P的坐标.
(3)该抛物线有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com