
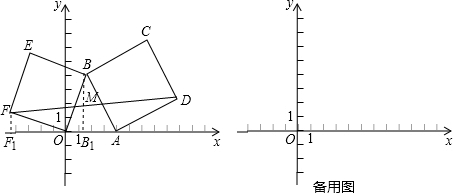
·ÖĪö £Ø1£©ČēĶ¼1ÖŠ£¬×÷DH”ĶxÖįÓŚH£®Ö»ŅŖÖ¤Ć÷”÷FOF1”Õ”÷OBB1£¬æɵĆFF1=OB1=m£¬OF1=BB1=n£¬ĶĘ³öF£Ø-n£¬m£©£¬Ķ¬·ØæɵƵćD×ų±ź£»
£Ø2£©¢ŁČēĶ¼2ÖŠ£¬ÉčM£Øx£¬y£©£®ĄūÓĆÖŠµć×ų±ź¹«Ź½¼“æɽā¾öĪŹĢā£»
¢ŚĒó³öĘšŹ¼µćMµÄ×ų±ź£¬ĄūÓĆĮ½µć¼ä¾ąĄė¹«Ź½¼“æɽā¾öĪŹĢā£»
½ā“š ½ā£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬×÷DH”ĶxÖįÓŚH£®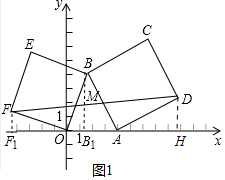
”ßĖıߊĪOBEFŹĒÕż·½ŠĪ£¬
”ąOB=OF£¬”ĻFOB=90”ć£¬
”ßFF1”ĶxÖį£¬BB1”ĶxÖį£¬
”ą”ĻFF1O=”ĻBB1O=90”ć£¬
”ą”ĻFOF1+”ĻBOB1=90”ć£¬”ĻBOB1+”ĻOBB1=90”ć£¬
”ą”÷FOF1”Õ”÷OBB1£¬
”ąFF1=OB1=m£¬OF1=BB1=n£¬
”ąF£Ø-n£¬m£©£¬
Ķ¬·ØæÉÖ¤BB1=AH=n£¬DH=AB1=a-m£¬
”ąD£Øa+n£¬a-m£©£¬
¹Ź“š°øĪŖ”÷FOF1£¬”÷OBB1£¬£Ø-n£¬m£©£¬£Øa+n£¬a-m£©£®
£Ø2£©¢ŁČēĶ¼2ÖŠ£¬ÉčM£Øx£¬y£©£®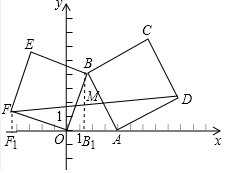
”ßF£Ø-n£¬m£©£¬D£Øa+n£¬a-m£©£¬FM=DM£¬
”ąx=$\frac{-n+a+n}{2}$£¬y=$\frac{m+a-m}{2}$£¬
”ąx=$\frac{a}{2}$£¬y=$\frac{a}{2}$£¬
”ąy=x£®
”ąµćM×ÜĀäŌŚŅ»øöŗÆŹżĶ¼ĻóÉĻ£¬øĆŗÆŹżµÄ½āĪöŹ½ĪŖy=x£®
¢Ś”ß2”Üa”Ü8£¬
”ąa=2Ź±£¬M£Ø1£¬1£©£¬
a=8Ź±£¬M£Ø4£¬4£©£¬
”ąµćMµÄŌĖ¶ÆĀ·¾¶µÄ³¤ĪŖ$\sqrt{£Ø4-1£©^{2}+£Ø4-1£©^{2}£©}$=3$\sqrt{2}$£®
µćĘĄ ±¾Ģāæ¼²éĖıߊĪ×ŪŗĻĢā”¢Õż·½ŠĪµÄŠŌÖŹ”¢Č«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢¹“¹É¶ØĄķ”¢ÖŠµć×ų±ź¹«Ź½”¢Į½µć¼ä¾ąĄė¹«Ź½µČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒÕżČ·Ń°ÕŅČ«µČČż½ĒŠĪ½ā¾öĪŹĢā£¬Įé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼³£æ¼ĢāŠĶ£®


 Õć½ĆūŠ£ĆūŹ¦½š¾ķĻµĮŠ“š°ø
Õć½ĆūŠ£ĆūŹ¦½š¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ¼×ĘļĦĶŠ³µ“ÓAµŲČ„BµŲ£®ŅŅæŖĘū³µ“ÓBµŲČ„AµŲ£®Ķ¬Ź±³ö·¢£¬ŌČĖŁŠŠŹ»£®ø÷×Ōµ½“ļÖÕµćŗóĶ£Ö¹£®Éč¼×”¢ŅŅĮ½ČĖ¼äµÄ¾ąĄėĪŖs£Øµ„Ī»£ŗĒ§Ć×£©£¬¼×ŠŠŹ»µÄŹ±¼äĪŖt£Øµ„Ī»£ŗŠ”Ź±£©£¬sÓėtÖ®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪÖŠ£¬“ķĪóµÄŹĒ£Ø””””£©
¼×ĘļĦĶŠ³µ“ÓAµŲČ„BµŲ£®ŅŅæŖĘū³µ“ÓBµŲČ„AµŲ£®Ķ¬Ź±³ö·¢£¬ŌČĖŁŠŠŹ»£®ø÷×Ōµ½“ļÖÕµćŗóĶ£Ö¹£®Éč¼×”¢ŅŅĮ½ČĖ¼äµÄ¾ąĄėĪŖs£Øµ„Ī»£ŗĒ§Ć×£©£¬¼×ŠŠŹ»µÄŹ±¼äĪŖt£Øµ„Ī»£ŗŠ”Ź±£©£¬sÓėtÖ®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪÖŠ£¬“ķĪóµÄŹĒ£Ø””””£©| A£® | ³ö·¢1Š”Ź±Ź±£¬¼×”¢ŅŅŌŚĶ¾ÖŠĻąÓö | |
| B£® | ³ö·¢1.5Š”Ź±Ź±£¬ŅŅ±Č¼×¶ąŠŠŹ»ĮĖ60Ē§Ć× | |
| C£® | ³ö·¢3Š”Ź±Ź±£¬¼×”¢ŅŅĶ¬Ź±µ½“ļÖÕµć | |
| D£® | ¼×µÄĖŁ¶ČŹĒŅŅĖŁ¶ČµÄŅ»°ė |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
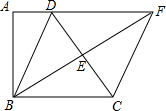 ČēĶ¼£¬ĖıߊĪABCDÖŠ£¬”ĻA=”ĻABC=90”ć£¬EŹĒ±ßCDµÄÖŠµć£¬Į¬½ÓBE²¢ŃÓ³¤ÓėADµÄŃÓ³¤ĻßĻą½»ÓŚµćF£®
ČēĶ¼£¬ĖıߊĪABCDÖŠ£¬”ĻA=”ĻABC=90”ć£¬EŹĒ±ßCDµÄÖŠµć£¬Į¬½ÓBE²¢ŃÓ³¤ÓėADµÄŃÓ³¤ĻßĻą½»ÓŚµćF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
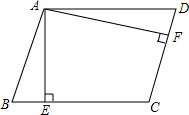 ČēĶ¼£¬Ę½ŠŠĖıߊĪABCDµÄĮŚ±ßAD£ŗAB=5£ŗ4£¬¹żµćA×÷AE”ĶBC£¬AF”ĶCD£¬“¹×ć·Ö±šĪŖµćE”¢F£¬AE=2cm£¬ŌņAF=2.5cm£®
ČēĶ¼£¬Ę½ŠŠĖıߊĪABCDµÄĮŚ±ßAD£ŗAB=5£ŗ4£¬¹żµćA×÷AE”ĶBC£¬AF”ĶCD£¬“¹×ć·Ö±šĪŖµćE”¢F£¬AE=2cm£¬ŌņAF=2.5cm£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com