
如图,已知抛物线的顶点为A(1,4)、抛物线
与y轴交于点B(0,3),与x轴交于C、D两点.
点P是x轴上的一个动点.
(1)求此抛物线的解析式.
(2)当PA+PB的值最小时,求点P的坐标.
 |
科目:初中数学 来源: 题型:
如图,反比例函数 和一次函数 的图象交于A、B两点. A、B两点的横坐标分别为2,-3.通过观察图象,
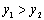 若 ,则x的取值范围是
若 ,则x的取值范围是
A. 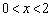 B.
B. 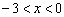 或
或 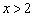
C. 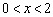 或
或 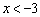 D.
D. 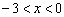
 |


查看答案和解析>>
科目:初中数学 来源: 题型:
财政部近日公开的情况显示. 2014年中央本级“三公”经费财政拨款预算比去年年初预算减少8.18亿元.用科学记数法表示为8.18亿元_______________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
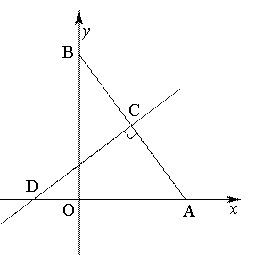
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程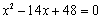 的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D.点P是直线CD上的一个动点,点Q是直线AB上的一个动点.
的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D.点P是直线CD上的一个动点,点Q是直线AB上的一个动点.
(1)求A、B两点的坐标;
(2)求直线CD的解析式;
(3)在坐标平面内是否存在点M,使以点C、P、Q、M为顶点的四边形是正方形,且该正方形的边长为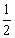 AB长.若存在,请直接写出点M的坐标;若不存在,请说明理由.
AB长.若存在,请直接写出点M的坐标;若不存在,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
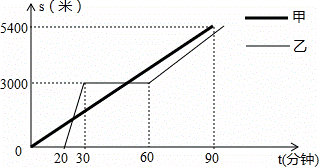
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:
(1)乙出发后多长时间与甲相遇?
(2)要使甲到达景点C时,乙与C的路程不超过400米,则乙从景点B步行到景点C的速度至少为 多少?(结果精确到0.1米/分钟)
多少?(结果精确到0.1米/分钟)
查看答案和解析>>
科目:初中数学 来源: 题型:
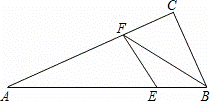
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. A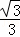 B.
B. 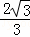 C.
C. 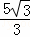 D.
D. 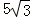
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com