
【题目】如图,在三角形ABC中,已知AC⊥BC,CD⊥AB,∠1=∠2.对于下列五个结论:
①DE∥AC;
②∠1=∠B;
③∠3=∠A;
④∠3=∠EDB;
⑤∠2与∠3互补.
其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
科目:初中数学 来源: 题型:
【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究

(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C=______;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案______.
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
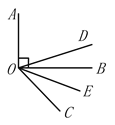
【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先完成下列表格:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
(2)由上表你发现什么规律?
(3)根据你发现的规律填空:
①已知![]() =1.732则
=1.732则![]() =______
=______![]() =______
=______
②已知![]() =0.056,则
=0.056,则![]() =______
=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.从盒中随机取一个球,它是黑球的概率是![]() ;往盒中再放进1个黑球,这时取得黑球的概率变为
;往盒中再放进1个黑球,这时取得黑球的概率变为![]() .
.
(1)试求出x和y的值;
(2)小王和小林利用x个黑球和y个白球进行摸球游戏.约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利.小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:
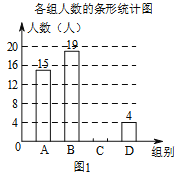
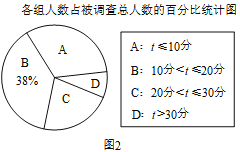
(1)这次被调查的总人数是______;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数;
(4)如果骑共享单车的平均速度为12km/h,请估算,在租用共享单车的市民中,骑车路程不超过6km的人数所占的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发公司计划建 A,B 两种户型的住房 80 套,该公司所筹资金不 少于 2090 万元,但不超过 2096 万元,且所筹金全部用于建房,两种户型的建房成 本和售价如下表:

(1)该公司对两种户型的住房有哪几种建房方案?
(2)该公司选用哪种建房方案获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
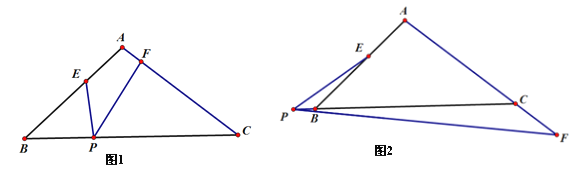
【题目】(1)如图1,△ABC中,∠BAC=100°,AB=AC,P为BC边上任意一点.若点E、F分别在AB、AC上,且∠EPF=40°,求证:△BPE∽△CFP;
(2)如图2,点P在边CB的延长线上,点E在边AB上,点F在边AC的延长线上,仍有∠EPF=40°,探索PB·PC与BE·CF有怎样的关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com