
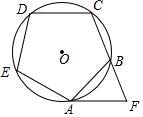
 如图,正五边形ABCD内接于⊙O,过点A的切线与CB的延长线相交于点F,则∠F=( )
如图,正五边形ABCD内接于⊙O,过点A的切线与CB的延长线相交于点F,则∠F=( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
分析 连接半径,由正五边形ABCDE计算其中心角∠AOB=$\frac{360}{5}$=72°,根据等腰三角形的两个底角相等求∠OAB=36°,由切线的直角得∠BAF的度数,根据五边形的外角=$\frac{360}{5}$=72°,由三角形的内角和定理得∠F的度数.
解答 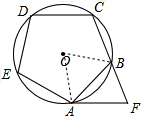 解:连接OA、OB,
解:连接OA、OB,
∵AF是⊙O的切线,
∴∠OAF=90°,
∵正五边形ABCDE内接于⊙O,
∴∠AOB=$\frac{360}{5}$=72°,
∵OA=OB,
∴∠OAB=∠OBA=$\frac{180-72}{2}$=54°,
∴∠BAF=90°-54°=36°,
∵∠ABF=$\frac{360}{5}$=72°,
∴∠F=180°-36°-72°=72°,
故选D.
点评 本题考查了三角形的内角和定理、正五边形的中心角和外角的求法,明确多边形的外角和为360°,正n边形的外接圆的中心角=$\frac{360}{n}$.


科目:初中数学 来源: 题型:选择题
| A. | -(2x-y)=-2x-y | B. | -3a+(4a2+2)=-3a+4a2-2 | ||
| C. | -(2a-3y)=-2a+3y | D. | -3(a-7)=-3a+7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 种植10棵幼树,结果一定是“有9棵幼树成活” | |
| B. | 种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活” | |
| C. | 种植10n棵幼树,恰好有“n棵幼树不成活” | |
| D. | 种植n棵幼树,当n越来越大时,种植成活幼树的频率会越来越稳定于0.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com