练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

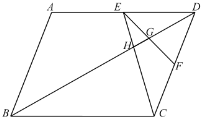
    【题目】如图，中，点、分别是边、的中点，、分别交对角线于点、，则______.

    【答案】

    【解析】

    由四边形ABCD是平行四边形可得AD∥BC，AD=BC，△DEH∽△BCH，进而得，连接AC，交BD于点M，如图，根据三角形的中位线定理可得EF∥AC，可推得，△EGH∽△CMH，于是得DG=MG，，设HG=a，依次用a的代数式表示出MH、DG、BH，进而可得答案.

    解：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，

    ∴△DEH∽△BCH，∵E是AD中点，AD=BC，∴，

    连接AC，交BD于点M，如图，∵点、分别是边、的中点，∴EF∥AC，

    ∴，△EGH∽△CMH，∴DG=MG，，

    设HG=a，则MH=2a，MG=3a，∴DG=3a，∴DM=6a，

    ∵四边形ABCD是平行四边形，∴BM=DM=6a，BH=8a，

    ∴.

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2-4x-3，下列说法中正确的是（ ）

    A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2，-7)

    C.当x<0时，y随x的增大而增大D.该函数图象与x轴有两个不同的交点，且分布在坐标原点两侧

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，与轴交于点，抛物线与直线交于，两点，点是抛物线的顶点．

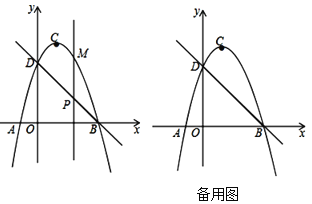
    （1）求抛物线的解析式；

    （2）点是直线上方抛物线上的一个动点，其横坐标为，过点作轴的垂线，交直线于点，当线段的长度最大时，求的值及的最大值．

    （3）在抛物线上是否存在异于、的点，使中边上的高为，若存在求出点的坐标；若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的半径为2，正八边形ABCDEFGH内接于⊙O，对角线CE、DF相交于点M，则△MEF的面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB＝AC＝2，∠BAC＝120°，D为BC边上的点，将DA绕D点逆时针旋转120°得到DE．

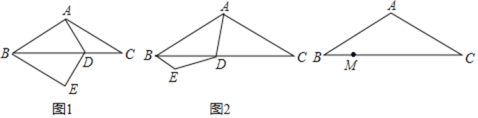
    （1）如图1，若AD＝DC，则BE的长为　 　，BE2+CD2与AD2的数量关系为　 　；

    （2）如图2，点D为BC边山任意一点，线段BE、CD、AD是否依然满足（1）中的关系，试证明；

    （3）M为线段BC上的点，BM＝1，经过B、E、D三点的圆最小时，记D点为D1，当D点从D1处运动到M处时，E点经过的路径长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场将进货单价为30元的商品以每个40元的价格售出时，平均每月能售出600个，调查表明：这种商品的售价每上涨1元，其销售量就减少10个.

    （1）为了使平均每月有10000元的销售利润且尽快售出，这种商品的售价应定为每个多少元？

    （2）当该商品的售价为每个多少元时，商场销售该商品的平均月利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE+FH的最大值为（ ）

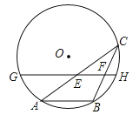
    A.8B.12C.16D.20

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题：

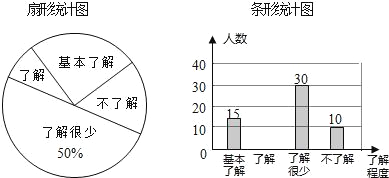
    （1）接受问卷调查的学生共有　 　人，扇形统计图中“基本了解”部分所对应扇形的圆心角为　 　度；

    （2）请补全条形统计图；

    （3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    材料1 若一元二次方程ax2+bx+c＝0（a≠0）的两个根为x1，x2则x1+x2＝﹣，x1x2＝．

    材料2 已知实数m，n满足m2﹣m﹣1＝0，n2﹣n﹣1＝0，且m≠n，求的值．

    解：由题知m，n是方程x2﹣x﹣1＝0的两个不相等的实数根，根据材料1得m+n＝1，mn＝﹣1，所以＝﹣3．

    根据上述材料解决以下问题：

    （1）材料理解：一元二次方程5x2+10x﹣1＝0的两个根为x1，x2，则x1+x2＝　 　，x1x2＝　 　．

    （2）类比探究：已知实数m，n满足7m2﹣7m﹣1＝0，7n2﹣7n﹣1＝0，且m≠n，求m2n+mn2的值：

    （3）思维拓展：已知实数s、t分别满足19s2+99s+1＝0，t2+99t+19＝0，且st≠1．求的值．

    查看答案和解析>>

    同步练习册答案