
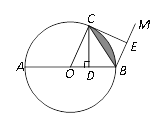
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D, 过点B作BM∥OC,在射线BM上取点E, 使BE=BD,连接CE.
(1) 当∠COB=60° 时,直接写出阴影部分的面积;
(2) 求证:CE是 ⊙O的切线.
【答案】(1) ![]() (2)证明见解析.
(2)证明见解析.
【解析】试题分析:(1)已知∠COB=60°,CD⊥AB,OA=OB=OC=2,可求得CD=![]() ,所以
,所以![]()
![]() ;(2)根据已知条件易证△CBD≌△CBE,可得∠CEB=∠CDB=90°,再由BM∥OC可得∠OCE+∠CEB=180°,即可得∠OCE=180°-∠CEB =180°-90°=90°,结论得证.
;(2)根据已知条件易证△CBD≌△CBE,可得∠CEB=∠CDB=90°,再由BM∥OC可得∠OCE+∠CEB=180°,即可得∠OCE=180°-∠CEB =180°-90°=90°,结论得证.
试题解析:
(1) ![]()
(2)证明:∵BM∥OC
∴∠OCB=∠CBE
∵OC=OB
∴∠OCB=∠OBC
∴∠OBC=∠CBE
又BD=BE, BC=BC
∴△CBD≌△CBE
∴∠CEB=∠CDB=90°
∵BM∥OC
∴ ∠OCE+∠CEB=180°
∴∠OCE=180°-∠CEB =180°-90°=90°
即OC⊥CE ∴CE是 ⊙O的切线.


科目:初中数学 来源: 题型:
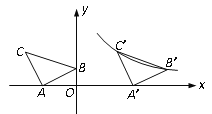
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
(1)点C的坐标是 ;
(2)将△ABC沿x轴正方向平移得到△A′ B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件羽绒服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利250元.若设这件羽绒服的成本是x元,根据题意,可得到的方程是( )
A.x(1+50%)×80%=x﹣250
B.x(1+50%)×80%=x+250
C.(1+50%x)×80%=x﹣250
D.(1+50%x)×80%=250﹣x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com