
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论: ①S1+S2=S3+S4;②S2+S4=S1+S3;③若S3=2S1 , 则S4=2S2;④若S1=S2 , 则P点在矩形的对角线上.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).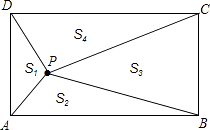
【答案】②和④
【解析】解:如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E, ∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3= ![]() 矩形ABCD面积;
矩形ABCD面积;
同理可得出S2+S4= ![]() 矩形ABCD面积;
矩形ABCD面积;
∴S2+S4=S1+S3(故②正确);
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4 . 但P是矩形ABCD内的任意一点,所以该等式不一定成立.(故①不一定正确);
③若S3=2S1 , 只能得出△APD与△PBC高度之比,S4不一定等于2S2;(故③错误);
④若S1=S2 , ![]() ×PF×AD=
×PF×AD= ![]() PE×AB,
PE×AB,
∴△APD与△PBA高度之比为: ![]() =
= ![]() ,
,
∵∠DAE=∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴此时矩形AEPF与矩形ABCD相似,
∴ ![]() =
= ![]() ,
,
∴P点在矩形的对角线上.(故④选项正确)
故答案为:②和④.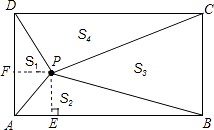
根据三角形面积求法以及矩形性质得出S1+S3= ![]() 矩形ABCD面积,以及
矩形ABCD面积,以及 ![]() =
= ![]() ,
, ![]() =
= ![]() ,即可得出P点一定在AC上.
,即可得出P点一定在AC上.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E. 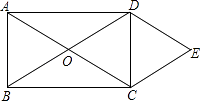
(1)求证:四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是边BC所在的直线上的动点(点D不与B、C重合),过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)求证:AF=DE;
(2)若AC=5,DE=6,则DF= .
(3)试探究:D在不同位置时,DE,DF,AC具有怎样的数量关系,直接写出结论:
①当点D在线段BC上时,关系是:;
②当点D在线段BC延长线上时,关系是:;
③当点D在线段CB延长线上时,关系是:;
(4)请选择(3)中你探究获得的其中一个结论证明之.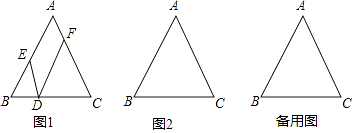
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )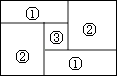
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
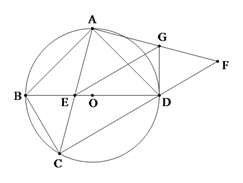
(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=2AD.
(1)作AE平分∠BAD交DC于E(尺规作图,保留作图痕迹);
(2)在(1)的条件下,连接BE,判定△ABE的形状(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,△ABC的三个顶点及D、E、F、G、H、五个点分别位于小正方形的顶点上. 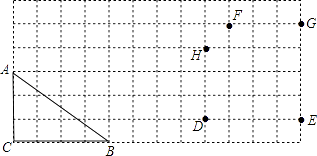
(1)画出△ABC绕点B顺时针方向旋转90°后的图形.
(2)先从E、F、G、H四个点中任意取两个不同的点,再和D点构成三角形,求所得三角形与△ABC面积相等的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com