
| 项目 | 跳绳 | 踢毽子 | 乒乓球 | 羽毛球 | 其他 |
| 人数(人) | 14 | 10 | 8 | 6 |

分析 (1)根据统计表以及扇形统计图中的数据进行计算,即可得到七年级抽查班级中喜欢“跳绳”项目的学生数,以及九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比;
(2)先根据条形统计图中的数据,求得八年级抽查班级中喜欢“踢毽子”项目的学生数,即可补全条形图;
(3)先求得九年级抽查班级中喜欢“羽毛球”项目的学生人数,结合七、八年级抽查班级中喜欢“羽毛球”项目的学生人数,即可估计该校喜欢“羽毛球”项目的学生总人数.
解答 解:(1)七年级抽查班级中喜欢“跳绳”项目的学生有50-14-10-8-6=12(人);
九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为1-28%-20%-18%-16%=18%;
故答案为:12,18%;
(2)八年级抽查班级中喜欢“踢毽子”项目的学生有50-15-9-9-7=10(人),
补全条形图如下: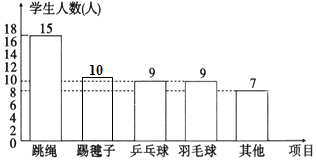
(3)九年级抽查班级中喜欢“羽毛球”项目的学生人数为50×20%=10(人),
3000×$\frac{8+9+10}{150}$=540(人),
故该校喜欢“羽毛球”项目的学生总人数为540人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
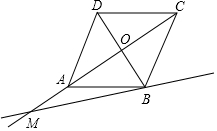 如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C,O,A都不重合),过点A,C分别向直线BM作垂线段,垂足分别为E,F,连接OE,OF.
如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C,O,A都不重合),过点A,C分别向直线BM作垂线段,垂足分别为E,F,连接OE,OF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.
如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com