
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.

(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PE的长.
【答案】(1)见解析;(2)PE=![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(2)由三角形中位线定理可得AE=2OF,由勾股定理可得AE=8,再由勾股定理可得PB的长.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
 ,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)∵点F为AB的中点,OB=OE,OF+OB=9,
∴AE=2OF,BE=2OB,AE+BE=18
设AE=x,BE=18-x,
∵BE2=AB2+AE2,
∴(18-x)2=36+x2,
∴x=8
∵AB2+AP2=PB2,
∴36+(8-PB)2=PB2,
∴PB=![]()
∴PE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,试说明:ME∥NF.
的角平分线,试说明:ME∥NF.
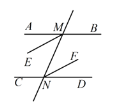
解:∵AB∥CD,(已知)
∴![]() ,( )
,( )
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,(已知)
的角平分线,(已知)
∴∠EMN= ∠AMN,
∠FNM= ∠DNM,(角平分线的定义)
∴![]() ,(等量代换)
,(等量代换)
∴ME∥NF,( )
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对 角的平分线互相 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与y轴的正半轴交于点A,其顶点B在
的图象与y轴的正半轴交于点A,其顶点B在![]() 轴的负半轴上,且OA=OB,对于下列结论:①
轴的负半轴上,且OA=OB,对于下列结论:①![]() ≥0;②
≥0;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 无实数根;④
无实数根;④![]() 的最小值为3.其中正确结论的个数为( )
的最小值为3.其中正确结论的个数为( )
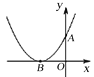
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
![]() 求实数
求实数![]() 的取值范围;
的取值范围;
![]() 是否存在实数
是否存在实数![]() ,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出
,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小立方块的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示,其中A、B、C、D、E、F分别代表数字-2、-1、0、1、2、3,则三个小立方块的下底面所标字母代表的数字的和为_____
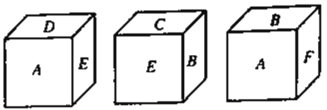
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
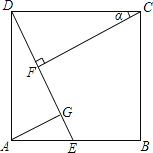
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“精准扶贫”这是新时期党和国家扶贫工作的精髓和亮点.某校团委随机抽取部分学生,对他们是否了解关于“精准扶贫”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:
(1)求本次活动共调查了 名学生;图1中,B区域的圆心角度是 ;在抽取的学生中调查结果的中位数落在 区域里.
(2)补全条形统计图.
(3)若该校有1200名学生,请估算该校不是了解很多的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是
是![]() 边所在直线上的点,
边所在直线上的点,![]() ,且
,且![]() 交正方形外角
交正方形外角![]() 的平分线
的平分线![]() 于点
于点![]() .
.
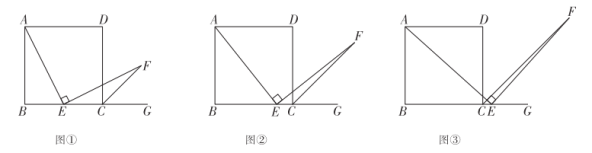
(1)当点![]() 在线段
在线段![]() 中点时(如图①),易证
中点时(如图①),易证![]() ,不需证明;
,不需证明;
(2)当点![]() 在线段
在线段![]() 上(如图②)或在线段
上(如图②)或在线段![]() 延长线上(如图③)时,(1)中的结论是否仍然成立?请写出你的猜想,并选择图②或图③的一种结论给予证明.
延长线上(如图③)时,(1)中的结论是否仍然成立?请写出你的猜想,并选择图②或图③的一种结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
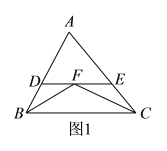
【题目】如图![]() ,在
,在![]() 中,
中,![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 相交于
相交于![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,通过上述条件,我们不难发现:
,通过上述条件,我们不难发现:![]() ;如图
;如图![]() ,
,![]() 的平分线
的平分线![]() 与
与![]() 的外角平分线
的外角平分线![]() 相交于
相交于![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() 根据图
根据图![]() 所得的结论,试猜想
所得的结论,试猜想![]() ,
,![]() ,
,![]() 之间存在什么关系?( )
之间存在什么关系?( )
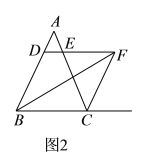
A. ![]() B.
B. ![]() C.
C. ![]() D. 无法判断
D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com